- UID
- 4922
- 注册时间
- 2014-4-13
- 在线时间
- 小时
- 最后登录
- 1970-1-1
- 精华
- 阅读权限
- 30
- 听众
- 收听
|
本文主要内容是四旋翼非线性模型的建立和底层飞控的设计。
本文不会展开去讲每个环节的细节,只是把最重要的部分罗列出来,使得读者能够以最快的速度在仿真环境中搭建自己的四旋翼模型,从而完成自己的任务需求。或者让读者有个大致的理解,去完成跟四旋翼有关的其他任务。
通过本文的阅读,读者应该能够了解以下内容:
- 四旋翼非线性模型和底层飞控的大致结构
- 哪些状态量能够完整表示四旋翼的运动
- 四旋翼底层飞控能够执行哪些指令
- 尝试搭建自己的四旋翼模型,并且能够实现飞轨迹
先给出四旋翼建模和底层飞控的整体结构图:

上层控制器给出底层的控制指令,例如轨迹规划、协同控制算法等都算是上层控制器。
1. 坐标系
1.1 坐标系定义
坐标系定义是最基础的前提,因为所有的公式变量都是以坐标系为前提的。
对于四旋翼模型来说,需要两个坐标系:
- 全局坐标系/大地坐标系/惯性坐标系,符号表示: \Sigma^\mathrm{g} - (NED北东地)
- 机体坐标系,符号表示: \Sigma^\mathrm{b} - (前右下)
全局坐标系是固连在大地上的;机体坐标系是固连到四旋翼机体上的,所以如果有很多个四旋翼,也就有很多个机体坐标系。
全局坐标系的原点一般来说是定义在飞机起飞点附近,在近距离的飞行时,可以忽略地球的曲率。机体坐标系的原点定义是飞机的重心位置。
全局坐标系的x,y,z轴的正方向分别是北东地(NED),所以无人机向上飞,其z轴坐标是负数。
机体坐标系的 x,y,z 轴的正方向分别是前右下,也就是飞机的正前方是x轴的正方向。
按照以上定义,如果全局坐标系的原点设在起飞点,无人机起飞前的初始位置的摆放是正前方对应北向,那么初始时,这两个坐标系是重合的。
1.2 坐标变换
首先定义3个旋转矩阵:
R_x = \left[ \begin{matrix}1 & 0 & 0 \\0 & \cos\theta_x & \sin\theta_x \\0 & -\sin\theta_x & \cos\theta_x\end{matrix}\right] ,
R_y = \left[ \begin{matrix}\cos\theta_y & 0 & -\sin\theta_y \\0 & 1 & 0 \\ \sin\theta_y & 0 & \cos\theta_y\end{matrix}\right] ,
R_z = \left[ \begin{matrix}\cos\theta_z & \sin\theta_z & 0 \\-\sin\theta_z & \cos\theta_z & 0 \\0 & 0 & 1\end{matrix}\right]
分别是绕x,y,z轴旋转 \theta 角的旋转矩阵。
- 全局到机体坐标变换公式为:P^b=R^{g2b}(P^g-T_{b}^g)
其中,
- P^g 是全局坐标系下的点的坐标,
- P^b 是同样的点在机体坐标系下的坐标;
- R^{g2b}=R_xR_yR_z ;
- 飞机角度为, \theta_x=roll, \theta_y=pitch,\theta_z=yaw ;
- T_b^g 为飞机全局坐标系下的位置。
- 机体到全局坐标变换公式为: P^g=R^{b2g}P^b+T_b^g
- 其中, R^{b2g}=(R^{g2b})^{-1}=R_zR_yR_x ;
- 飞机角度为 \theta_x=-roll, \theta_y=-pitch,\theta_z=-yaw
坐标变换有两种变换方法:先平移后旋转;先旋转后平移。
上面全局到机体的变换是先平移后旋转的方式,而机体到全局的变换是先旋转后平移的方式。两种方式都可以。
注意上面的变换中,从全局到机体和从机体到全局的变换是互逆的,两个旋转矩阵也是互逆的。但是如果两种变换都是用同样的方式(比如先旋转后平移),那么两个旋转矩阵就不是互逆的了。
1.3 坐标变换的通俗解释
这一节是一个非常通俗的坐标变换的解释,对坐标变换比较熟悉的读者就不需要看了。
可能刚开始接触坐标系转换的同学对各种旋转矩阵搞得很头疼,其实只要搞明白源头,搞明白为什么要进行坐标系变换,搞明白坐标系变换的本质,就不难理解了。
其实说白了,坐标系变换就是用不同的方式来表示同一个点。让我们首先通俗的讲一下这个事情,我想表示二维平面中某一个点,这时我可以用手指或者画一个箭头指向这个点,那你就知道了我想表达的这个点了。但是如果有很多点怎么办,我如果对每一个点都画个箭头,那么就太乱了,这时,坐标系就出现了。我可以首先建立一个坐标,确定了原点所在的位置和两个轴的方向,然后我把这个坐标系告诉你,这样咱俩都知道了同一个坐标系,以后再相互表达某些点的时候,只需要讲这些点的坐标就可以了,你可以根据坐标,在提前商量好的坐标系中快速地找到这些点。但是,如果你和我都有自己喜欢的坐标系,而且这两个坐标系不一样,不是同一个坐标系,那么我将某个点的坐标告诉你,你在你喜欢的坐标系上是无法准确找到这个点的,这时就需要坐标变换了。所以坐标变换就是用不同的坐标系去表达同一个点。
2. 四旋翼建模
2.1 四旋翼的状态量
首先我们使用到的四旋翼的状态量有18个量:
- 位置(全局坐标系): \bold{p}^\mathrm{g}=[x,y,z]^T ,
- 速度(全局坐标系): \bold{v}^\mathrm{g} = [v_x,v_y,v_z]^T
- 加速度(全局坐标系): \bold{a}^\mathrm{g}=[a_x,a_y,a_z]^T ,
- 姿态角: \Theta =[\phi,\theta,\psi]^T , (roll, pitch, yaw)
- 机体旋转角速度: \bold{\omega}^b=[p,q,r]^T ,
- 机体旋转角加速度: \bold{\dot{\omega}}^b=[\dot{p},\dot{q},\dot{r}]^T ,
其中姿态角是机体坐标系相对于全局坐标系的三个欧拉角,机体角速度和机体角加速度都是机体坐标系下的。
2.2 四旋翼6自由度模型 - 动力学模型与运动学模型
四旋翼非线性建模分为运动学模型和动力学模型两部分。6自由度模型的意思是四旋翼有6个自由度,分别是3个方向的移动和3个方向的转动。下面将6自由度模型的公式罗列出来,本文不进行细节方面详细的讲解,只讲明白怎么使用。
\begin{aligned} \bold{\dot{p}}^g&=\bold{v}^g \\ \bold{\dot{\Theta}}&=\bold{W}\cdot \bold{\omega}^b \end{aligned}
\begin{aligned} \bold{\dot{v}}&=g\bold{e}_3-\dfrac{f}{m}\bold{R}^{b2g}\bold{e}_3\\ \bold{J}\cdot \dot{\bold{\omega}}^b&=-\bold{\omega}^b\times(\bold{J}\cdot\bold{\omega}^b)+\bold{G}_a+\bold{\bold{\tau}} \end{aligned}
- 其中符号的解释
- \bold{p}^g 和 \bold{v}^g 分别是飞机的全局位置和全局速度;
- \bold{W} 是表示姿态角速率与机体角速度之间关系的矩阵, \bold{W}= \left[ \begin{matrix} 1 & \tan\theta \sin\phi & \tan\theta\cos\phi \\ 0 & \cos\phi & -\sin\phi \\ 0 & \sin\phi/\cos\theta & \cos\phi/\cos\theta \end{matrix} \right]
应避免 \cos\theta=0 的情况发生。
反过来可以得到: \bold{\omega}^b=\bold{W}^{-1}\dot{\Theta},
\bold{W}^{-1}=2\left[3\begin{matrix}41 & 0 & -\sin\theta \\50 & \cos\phi & \cos\theta\sin\phi \\60 & -\sin\phi & \cos\theta\cos\phi7\end{matrix}8\right]
- \dot{\bold{\Theta}} 是姿态角速率, \omega^b 是机体角速度;
- \bold{e}_3=[0,0,1]^T 表示单位列向量;
- f 是四个电机的拉力总和,方向沿机体坐标系z轴负方向;
- \bold{J} 是四旋翼的惯性矩阵, \bold{J}=diag(J_x,J_y,J_z) ;
- \bold{G}_a 表示陀螺力矩,一般忽略不计;
- \bold{\tau}=[\tau_x,\tau_y,\tau_z] 表示螺旋桨在机体轴上产生的外力矩。
2.3 四旋翼6自由度模型的使用
有了6自由度模型,输入飞机的整体拉力( f )和3个方向的力矩( \tau ),再加上上一时刻四旋翼的状态,就可以计算出下一时刻四旋翼的状态量(位置、速度、加速度、姿态角、机体角速率、机体角加速度)。
从写代码的计算过程来看,先使用动力学模型两个公式,输入拉力和力矩( f , \tau ),计算飞机的加速度( \bold{\dot{v}} )和角加速度( \dot{\bold{\omega}}^b ),然后再使用运动学模型的两个公式,更新其他状态量。
2.4 四旋翼电机模型
电机模型是用来对电机建模的,因为电机的响应非常快,所以可以忽略电机的延迟,等效认为对电机的转速指令能够瞬间达到。
四旋翼分为X型和十字型,分析过程相似,本文使用X型四旋翼来推导,
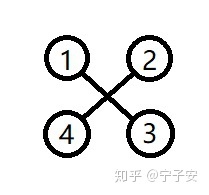
\begin{aligned} f&=c_T(\omega_1^2+\omega_2^2+\omega_3^2+\omega_4^2)\\ \tau_x &=lc_T(\dfrac{\sqrt{2}}{2}\omega_1^2-\dfrac{\sqrt{2}}{2}\omega_2^2-\dfrac{\sqrt{2}}{2}\omega_3^2+\dfrac{\sqrt{2}}{2}\omega_4^2) \\ \tau_y &=lc_T(\dfrac{\sqrt{2}}{2}\omega_1^2+\dfrac{\sqrt{2}}{2}\omega_2^2-\dfrac{\sqrt{2}}{2}\omega_3^2-\dfrac{\sqrt{2}}{2}\omega_4^2)\\ \tau_z &= c_M(\omega_1^2-\omega_2^2+\omega_3^2-\omega_4^2) \end{aligned}
其中, l 为机体中心到任一电机的距离, c_T 为拉力系数, c_M 为扭矩系数。
3. 四旋翼底层飞控
3.1 四旋翼底层飞控结构图
一般四旋翼的底层飞控都是用PID控制器,我这里在内环姿态回路用了LQR控制器,底层控制器整体结构图如下:
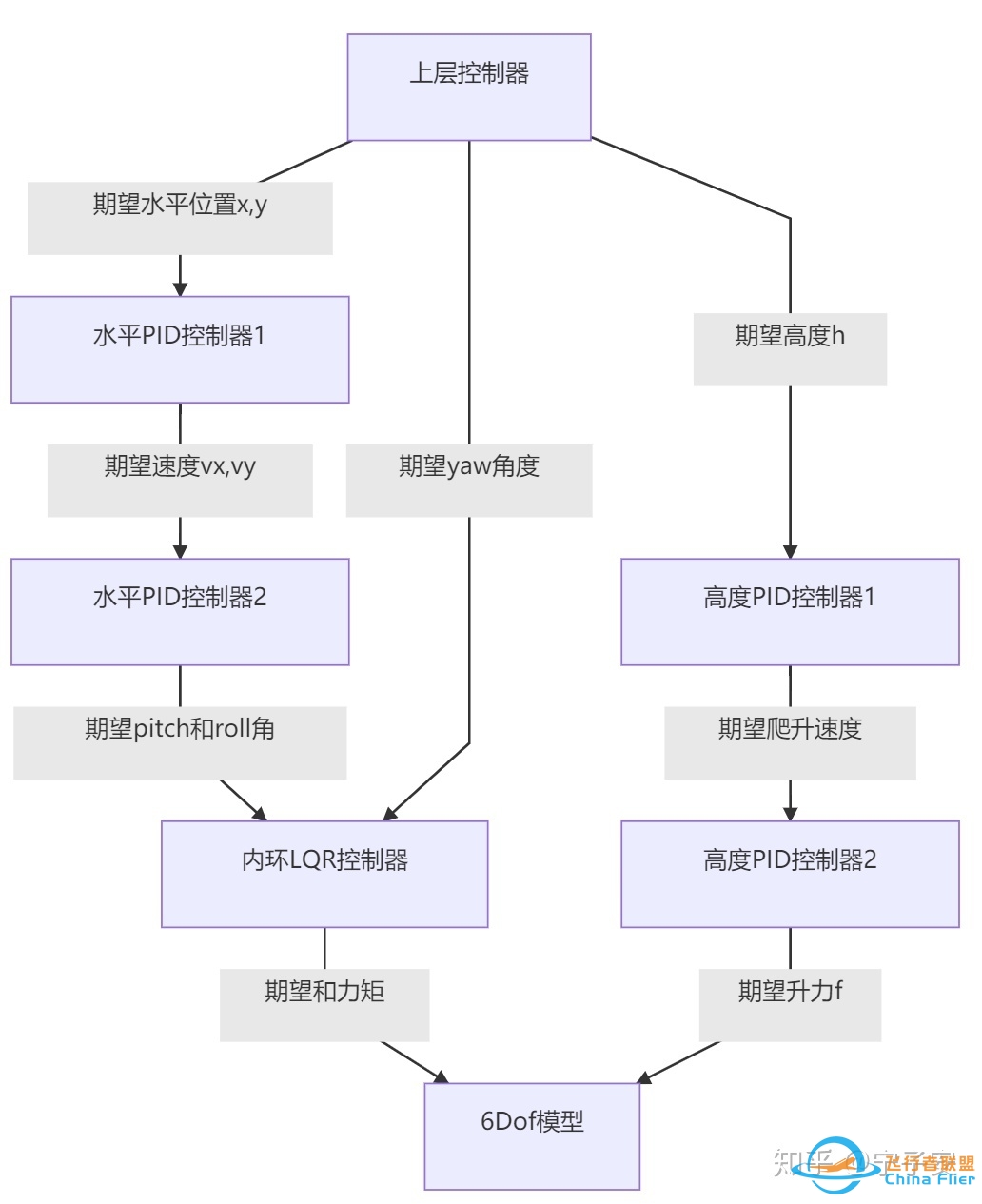
3.2 简化的线性模型
在设计控制器之前,首先要对6自由度非线性模型进行线性化,这样设计出来控制器以后,可以先用线性化的模型计算控制器的收敛性,以此判断控制设计的好不好。最后再用设计好的控制器去控制非线性模型。
- 假设条件:
- 动力学模型忽略 -\bold{\omega}^b\times(\bold{J}\cdot\bold{\omega}^b)+\bold{G}_a ;
- 俯仰角和滚转角都非常小:
- \sin(\phi)\approx \phi
- \cos(\phi)\approx 1
- \sin(\theta)\approx \theta
- \cos(\theta)\approx 1
- 总拉力约等于四旋翼的重力: f\approx mg
- 此时,运动学模型中的 \bold{W}\approx\bold{I}_3
- 此时,动力学模型中的 \bold{R}^{b2g}\bold{e}_3\approx \left[\begin{matrix} \theta\cos\psi+\phi\sin\psi \\ \theta\sin\psi-\phi\cos\psi \\ 1 \end{matrix}\right]
最终,忽略高阶项,原始模型解耦为三个线性模型:水平位置通道模型、高度通道模型、姿态模型
- 水平位置通道模型: \left\{\begin{aligned} \dot{\bold{p}}_h &= \bold{v}_h \\ \dot{\bold{v}}_h &= -g\bold{A}_\psi\bold{\Theta}_h \end{aligned}\right.
其中, \bold{p}_h=\left[\begin{matrix}x\\y\end{matrix}\right] , \bold{A}_\psi=\left[\begin{matrix}\sin\psi & \cos\psi \\ -\cos\psi & \sin\psi\end{matrix}\right] , \bold{\Theta}_h=\left[\begin{matrix}\phi\\ \theta\end{matrix}\right] .
- 高度通道模型: \left\{\begin{aligned} \dot{z} &= v_z \\ \dot{v}_z &= g-\dfrac{f}{m} \end{aligned}\right.
- 姿态模型: \left\{\begin{aligned} \dot{\bold{\Theta}} &= \bold{\omega} \\ \bold{J}\dot{\bold{\omega}} &= \bold{\tau} \end{aligned}\right.
3.3 外环PID控制器
外环PID分为水平和垂直两个解耦的控制器。
外环水平通道PID控制器
外环水平通道控制器有三种情况:输入指令可以是,位置、速度、加速度。
- 输入:期望水平方向的指令(三选一)位置、速度、加速度, (p_h)_{cmd}=[x_{cmd},y_{cmd}]^T , (\bold{v}_h)_{cmd}=[(v_x)_{cmd},(v_y)_{cmd}]^T , (a_h)_{cmd}=[(a_x)_{cmd},(a_y)_{cmd}]^T ;
- 输出(给内环):期望俯仰和滚转姿态角 \phi_{des},\theta_{des} ;
- 控制器设计:
- 位置控制:
- (\bold{v}_h)_{des}=\bold{K}_{p_h}\left((\bold{p}_h)_{cmd}-\bold{p}_h\right) , P控制器, 其中 (\bold{v}_h)_{des} 要限幅
- (\bold{a}_h)_{des}=(\bold{K}_{\bold{v}_hp}\bold{e}_{\bold{v}_h}+\bold{K}_{\bold{v}_hi}\int\bold{e}_{\bold{v}_h}+\bold{K}_{\bold{v}_hd}\dot{\bold{e}}_{\bold{v}_h}) , PID控制器,一般用PI即可,其中 (\bold{a}_h)_{des} 要限幅
- (\bold{\Theta}_h)_{des}=g^{-1}\bold{A}_\psi^{-1}(-\bold{a}_h)_{des} , 其中 (\bold{\Theta}_h)_{des} 要限幅。
- 其中 \bold{K}_{p_h},\bold{K}_{\bold{v}_hp},\bold{K}_{\bold{v}_hi},\bold{K}_{\bold{v}_hd}\in R^{2\times2} 是系数;\bold{e}_{\bold{v}_h}=(\bold{v}_h)_{des}-\bold{v}_h.
- 速度控制:
- (\bold{a}_h)_{des}=(\bold{K}_{\bold{v}_hp}\bold{e}_{\bold{v}_h}+\bold{K}_{\bold{v}_hi}\int\bold{e}_{\bold{v}_h}+\bold{K}_{\bold{v}_hd}\dot{\bold{e}}_{\bold{v}_h}) , PID控制器,一般用PI即可,其中 (\bold{a}_h)_{des} 要限幅
- (\bold{\Theta}_h)_{des}=-g^{-1}\bold{A}_\psi^{-1}(\bold{a}_h)_{des} , 其中 (\bold{\Theta}_h)_{des} 要限幅。
- 其中, \bold{K}_{\bold{v}_hp},\bold{K}_{\bold{v}_hi},\bold{K}_{\bold{v}_hd}\in R^{2\times2} 是系数; \bold{e}_{\bold{v}_h}=(\bold{v}_h)_{cmd}-\bold{v}_h .
- 加速度控制:
- (\bold{\Theta}_h)_{des}=-g^{-1}\bold{A}_\psi^{-1}(\bold{a}_h)_{cmd} , 其中 (\bold{\Theta}_h)_{des} 要限幅。
- 限幅:
- 输入限幅: ||(\bold{v}_h)_{des}||\le \max v_h ;
- 输出限幅: \phi_{des},\theta_{des}\le \max \theta .
外环高度通道PID控制器
- 输入:期望高度 z_{des} ;
- 输出:拉力 f_{des} ;
- 控制器设计: f_{des}=m(g+k_{v_zp}e_{v_z}+k_{v_zi}\int e_{v_z})
其中, k_{v_zp} , k_{v_zi} 是系数, e_{v_z}=v_z-(v_z)_{des} 是速度差,
其中, (v_z)_{des}=-k_z(z-z_{des}) .
- 限幅: (v_z)_{des}\le\max z_v , f_{des}\le\max f .
3.4 内环LQR控制器
输入输出
- 输入1(外环):期望的俯仰滚转角, \phi_{des},\theta_{des} ;
- 输入2:期望的偏航角 \psi_{des} ;
- 输出:力矩, \bold{\tau}_{des} .
控制器设计
- 状态方程:
\left[\begin{matrix} \dot{\phi} \\ \dot{\theta} \\ \dot{\psi} \\ \dot{p}\\ \dot{q}\\ \dot{r} \end{matrix}\right]= \left[\begin{matrix} 0&0&0&1 & \tan\theta \sin\phi & \tan\theta\cos\phi \\ 0&0&0&0 & \cos\phi & -\sin\phi \\ 0&0&0&0 & \sin\phi/\cos\theta & \cos\phi/\cos\theta \\ 0&0&0&0&0&0\\ 0&0&0&0&0&0\\ 0&0&0&0&0&0 \end{matrix}\right] \left[\begin{matrix} \phi \\ \theta \\ \psi \\ p\\ q\\ r \end{matrix}\right]+ \left[\begin{matrix} 0&0&0\\ 0&0&0\\ 0&0&0\\ 1/J_x&0&0 \\ 0& 1/J_y & 0\\ 0&0&1/J_z \end{matrix}\right] \left[\begin{matrix} \tau_x\\ \tau_y\\ \tau_z \end{matrix}\right]
\dot{x}=Ax+Bu
- 其中, x=[\phi,\theta,\psi,p,q,r]^T ;
- u=[\tau_x,\tau_y,\tau_z]^T ;
- A=\left[\begin{matrix}\bold{0}&\bold{W}\\\bold{0}&\bold{0}\end{matrix}\right] ;
- B=\left[\begin{matrix}\bold{0}\\ \bold{J}^{-1}\end{matrix}\right]
- 两个矩阵的参数选择: Q=diag\{8,8,2, 2, 2, 0.1\} , R=diag\{1,1,1\} ,
- 求中间矩阵 P ,解方程: A^TP+PA+Q-PBR^{-1}B^TP=0 ,
- 解出系数矩阵 K : K=R^{-1}B^TP ,
- 最后的解为:
\bold{\tau}_{des}=-K(x-x_{des})
- 限幅: \phi_{des},\theta_{des} \le \max\theta , \tau_{des}\le \max \tau
4. 四旋翼参数参考
下面列举的参数是我再仿真中用的参数,可以用来参考。
| 参数 | 数据 值/范围 | | 质量(kg) | 1.4 | | 轴距 (m) | 0.56 | | 转动惯量 (x,y,z) (kg/m^2) | [0.05,0.05,0.24] | | 滚转和俯仰角 | -30 ~ 30 | | 拉力 (N) | 0 ~ 43.5 | | 力矩 (x,y) (N.m) | -6.25 ~ 6.25 | | 力矩 z | -2.25 ~ 2.25 |
|
|