- UID
- 4871
- 注册时间
- 2014-4-10
- 在线时间
- 小时
- 最后登录
- 1970-1-1
- 精华
- 阅读权限
- 30
- 听众
- 收听
|
一、主要内容
本文旨在基于牛顿-欧拉方程建立四旋翼飞行器的动力学和运动学模型,从而得到四旋翼飞行器的飞行控制刚体模型。包括以下内容:
- 主要内容
- 基本假设
- 动力学模型与运动学模型
- 地球坐标系与机体坐标系
- 旋转矩阵
- 牛顿-欧拉方程
- 四旋翼飞行器的动力学模型
- 四旋翼飞行器的运动学模型
- 四旋翼飞行器的飞行控制刚体模型
二、基本假设
为便于建立模型,现对四旋翼飞行器进行以下假设[1]:
- 四旋翼飞行器是均匀对称的刚体
- 四旋翼飞行器的质量和转动惯量不发生改变
- 四旋翼飞行器的几何中心与其重心重合
- 四旋翼飞行器只受重力和螺旋桨拉力
- 螺旋桨1、3为逆时针转动,螺旋桨2、4为顺时针转动
三、动力学模型与运动学模型
建立四旋翼飞行器模型的目的在于分析四旋翼飞行器在受到外力、外力矩的情况下,其位置和姿态的变化情况。
其中,动力学模型的输入为螺旋桨提供的拉力和力矩,输出为四旋翼的速度和角速度;运动学模型的输入为动力学模型的输出,即四旋翼的速度和角速度,输出为四旋翼的位置和姿态。
其关系如下图所示:

图1 四旋翼飞行器的飞行控制刚体模型
四、地球坐标系与机体坐标系
在建立模型之前,需要先对表示向量的坐标系进行定义。本文将用到两个坐标系,即惯性坐标系(静坐标系)——地球坐标系,以及非惯性坐标系(动坐标系)——机体坐标系。
地球坐标系取地球中心为坐标原点,其与地球固连。
机体坐标系取飞行器重心位置为坐标原点,其与四旋翼飞行器固连, O_bx_b 轴方向为飞行器前进方向。
如下图所示:
图2 地球坐标系与机体坐标系
图中, O_ex_ey_ez_e 为地球坐标系, O_bx_by_bz_b 为机体坐标系。
两个坐标系都遵循右手法则,关于右手定则的具体内容见下图[1]所示,这里截取的是北航全权老师所著的《多旋翼飞行器设计与控制》中的部分内容。

图3 右手定则
注:在有些论文资料中,将地球坐标系中的 O_ez_e 轴和机体坐标系中的 O_bz_b 轴的方向定义为向上为正,与图2所示方向刚好相反,如图4[2]所示。这并不影响建模过程,只影响动力学方程的正负号。
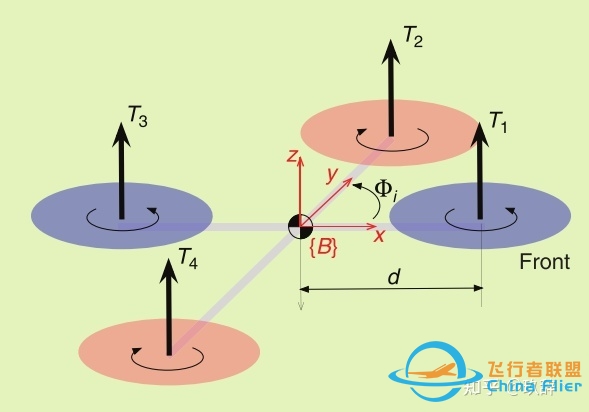
图4 Oz轴定义为垂直于xy平面向上
五、旋转矩阵
旋转矩阵的作用是将机体坐标系下表示的向量转变到地球坐标系下表示,向量的本质并不发生任何改变,只是改变了向量的表达形式。
旋转矩阵改变向量表达形式的目的在于[1]:
- 在地球坐标系下表示四旋翼飞行器的位置和速度,有助于飞控手更好地确定飞行器的位置和飞行速度;
- 在机体坐标系下表示四旋翼飞行器的拉力和力矩比较直观,且传感器的测量也是在机体坐标系下表示的。
旋转矩阵的推导过程可以参见下面这两篇文章,本文直接给出旋转矩阵的结果。
任一向量从机体坐标系 O_bx_by_bz_b 到地球坐标系 O_ex_ey_ez_e 的旋转矩阵表示为:
\boldsymbol{R}_{b}^{e}=\left[ \begin{matrix} \cos \theta \cos \psi& \cos \psi \sin \theta \sin \phi -\sin \psi \cos \phi& \cos \psi \sin \theta \cos \phi +\sin \psi \sin \phi\\ \cos \theta \sin \psi& \sin \psi \sin \theta \sin \phi +\cos \psi \cos \phi& \sin \psi \sin \theta \cos \phi -\cos \psi \sin \phi\\ -\sin \theta& \sin \phi \cos \theta& \cos \phi \cos \theta\\ \end{matrix} \right]
式中, \boldsymbol{R}_{b}^{e} 右下方的 b 表示机体坐标系,右上方的 e 表示地球坐标系; \phi , \theta , \psi 分别表示绕 x 轴旋转的滚转角、绕 y 轴旋转的俯仰角以及绕 z 轴旋转的偏航角,即欧拉角,如下图所示:
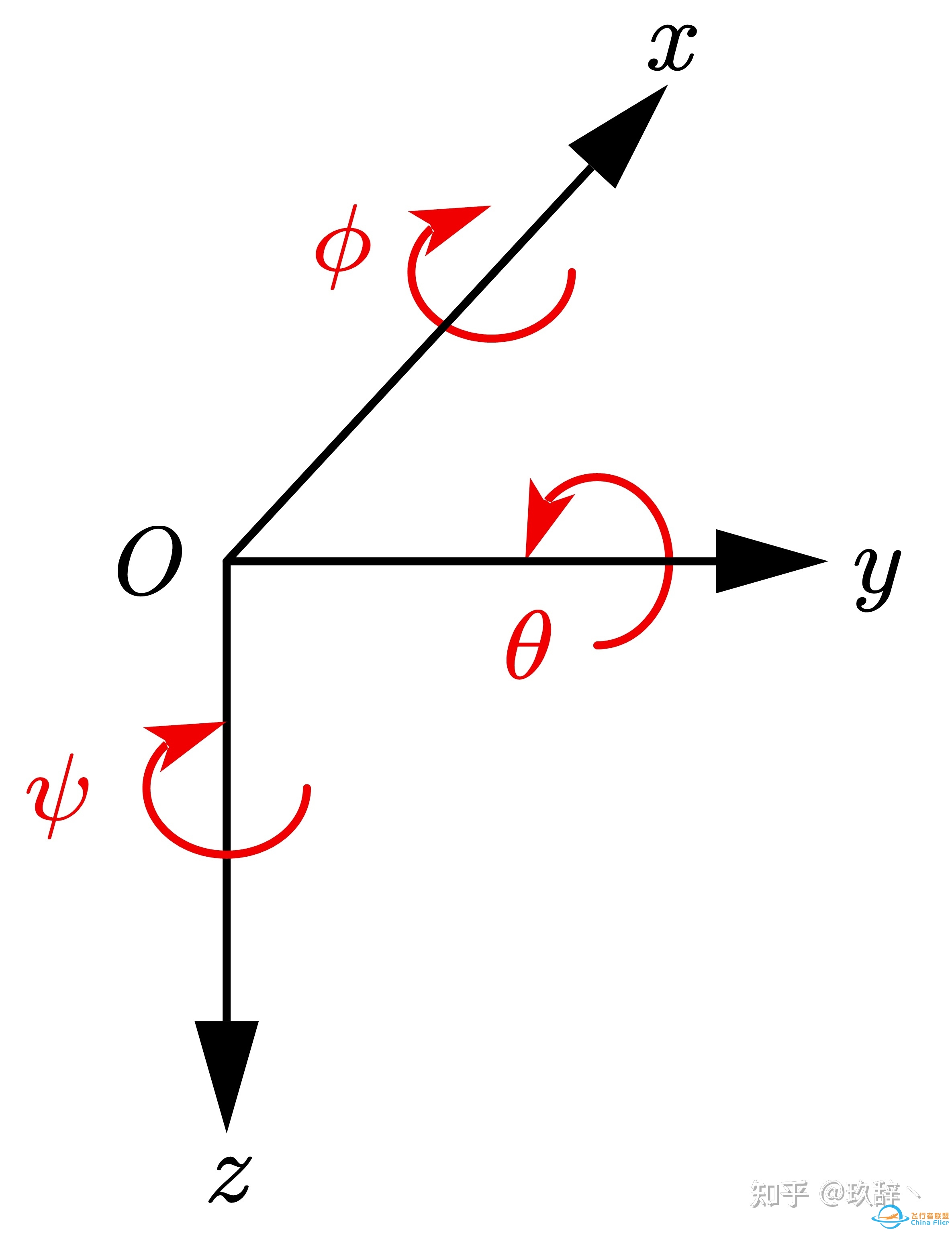
图5 欧拉角的定义
六、牛顿-欧拉方程
由牛顿-欧拉方程可知,刚体运动=质心的平动+绕质心的转动
质心的平动用牛顿第二定律描述,即:
\boldsymbol{F}=m\frac{d\boldsymbol{v}}{dt} (1)
式中, \boldsymbol{F} 为刚体所受合外力; \boldsymbol{v} 为刚体的运动速度。
绕质心的转动由欧拉方程描述,即:
\boldsymbol{M}=\boldsymbol{J\dot{\omega}}+\boldsymbol{\omega }\times \boldsymbol{J\omega } (2)
式中 , \boldsymbol{M}为刚体所受的合外力矩; \boldsymbol{J} 为3×3的惯性矩阵; \boldsymbol{\omega } 为刚体的角速度。
其表达的含义为:作用在刚体上的合力矩 \boldsymbol{M} 使得刚体以角速度 \boldsymbol{\omega } 、角加速度 \boldsymbol{\dot{\omega}} 旋转。
注:
2. (2)式中的“×”表示的是叉乘。若存在两个向量 \boldsymbol{a}=\left[ \begin{matrix} a_x& a_y& a_z\\ \end{matrix} \right] ^T 和 \boldsymbol{b}=\left[ \begin{matrix} b_x& b_y& b_z\\ \end{matrix} \right] ^T ,则有:
\boldsymbol{a}\times \boldsymbol{b}=\left[ \begin{matrix} 0& -a_z& a_y\\ a_z& 0& -a_x\\ -a_y& a_x& 0\\ \end{matrix} \right] \left[ \begin{array}{c} b_x\\ b_y\\ b_z\\ \end{array} \right] =\left[ \begin{array}{c} a_yb_z-a_zb_y\\ a_zb_x-a_xb_z\\ a_xb_y-a_yb_x\\ \end{array} \right]
其中,矩阵
\left[ \begin{matrix} 0& -a_z& a_y\\ a_z& 0& -a_x\\ -a_y& a_x& 0\\ \end{matrix} \right] 可记为 \left[ \boldsymbol{a} \right] _{\times} ,它是一个反对称矩阵。
七、四旋翼飞行器的动力学模型
此时便可以根据牛顿-欧拉方程建立四旋翼的动力学模型了。
动力学模型的输入为合外力、合外力矩,输出为速度、角速度。在(二)中,我们假设了飞行器只受重力和螺旋桨拉力,如下图所示:
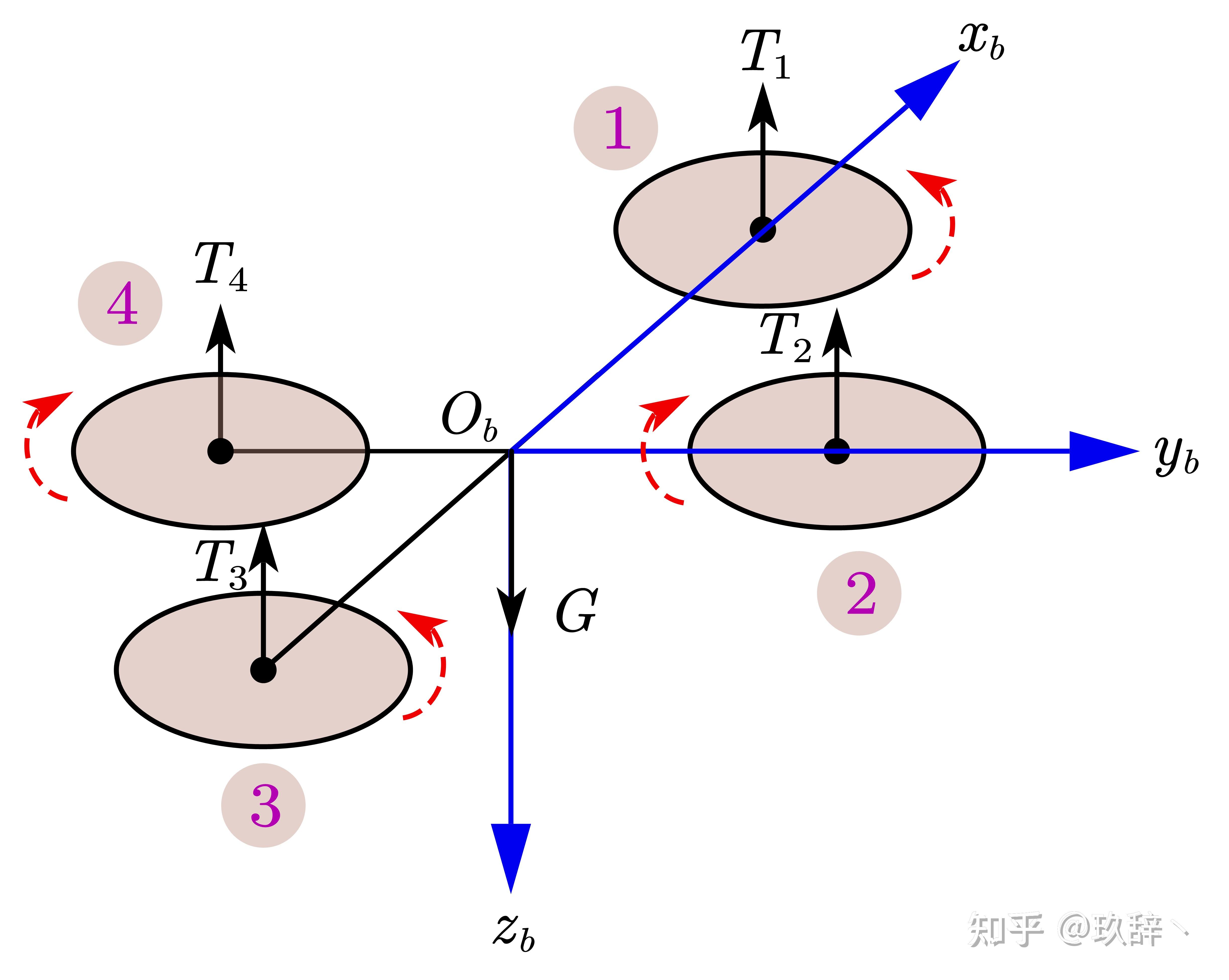
图6 四旋翼飞行器的受力情况
其中, T_1, T_2, T_3, T_4 分别为螺旋桨1、2、3、4所产生的拉力,由于假设了四旋翼飞行器是均匀对称的刚体,所以它们的合力——总拉力 f 过 O_b 点,且始终与 O_bz_b 轴的负方向一致。
1.位置动力学模型
由牛顿第二定律(1),有:
m\boldsymbol{\dot{v}}^e=\boldsymbol{G}^e-\boldsymbol{f}^b (3)
式中, \boldsymbol{v}, \boldsymbol{G} 右上角的字母 e 代表这是在地球坐标系下表示的向量; \boldsymbol{f} 右上角的字母 b 代表这是在机体坐标系下表示的向量。由于拉力是由螺旋桨产生的,与四旋翼飞行器固连,故在机体坐标系下表示。
等式两边同时除以质量,得:
\boldsymbol{\dot{v}}^e=\boldsymbol{g}^e-\frac{\boldsymbol{f}^b}{m} (4)
为了便于研究,将拉力转换至地球坐标系下表示,左乘旋转矩阵 \boldsymbol{R}_{b}^{e} 即可:
\boldsymbol{\dot{v}}^e=\boldsymbol{g}^e-\boldsymbol{R}_{b}^{e}\frac{\boldsymbol{f}^b}{m} (5)
四旋翼飞行器的重力和拉力都是沿着O_ez_e轴的,故有:
\boldsymbol{\dot{v}}^e={g}\boldsymbol{e}_3-\frac{{f}}{m}\boldsymbol{R}_{b}^{e}\boldsymbol{e}_3 (6)
式中, \boldsymbol{e}_3 是沿着地球坐标系中 O_ez_e 轴的单位向量,如下图所示:
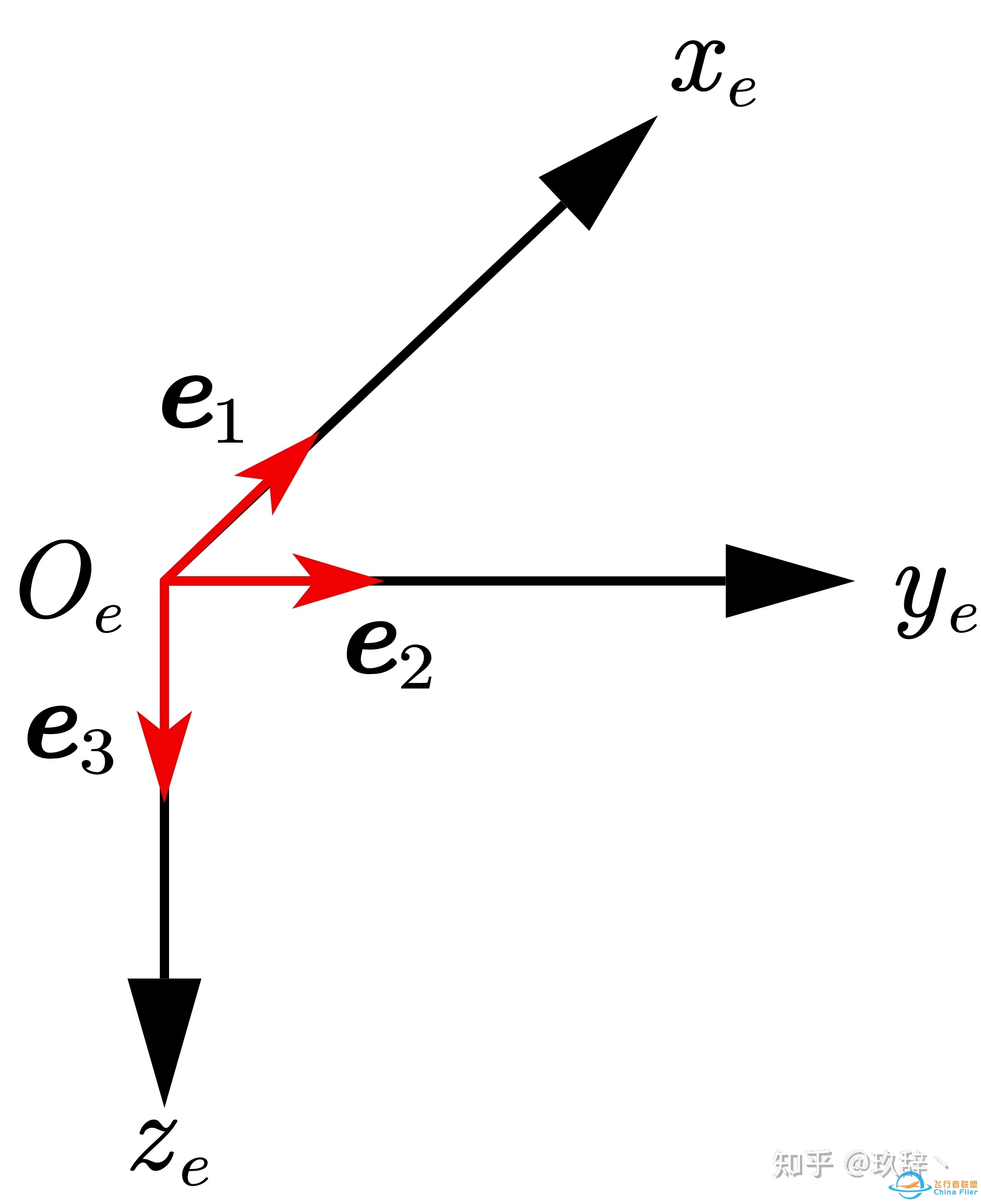
图7 地球坐标系下的单位向量
且有:
\boldsymbol{e}_1=\left[ \begin{array}{c} 1\\ 0\\ 0\\ \end{array} \right] , \boldsymbol{e}_2=\left[ \begin{array}{c} 0\\ 1\\ 0\\ \end{array} \right] , \boldsymbol{e}_3=\left[ \begin{array}{c} 0\\ 0\\ 1\\ \end{array} \right]
此时,将(6)式展开,并将 \boldsymbol{R}_{b}^{e} 、 \boldsymbol{e}_3 代入可得:
\left[ \begin{array}{c} {\dot{v}}_x\\ {\dot{v}}_y\\ {\dot{v}}_z\\ \end{array} \right] ={g}\left[ \begin{array}{c} 0\\ 0\\ 1\\ \end{array} \right] -\frac{{f}}{m}\boldsymbol{R}_{b}^{e}\left[ \begin{array}{c} 0\\ 0\\ 1\\ \end{array} \right] \\ \Downarrow \\ \begin{cases} {\dot{v}}_x=-\frac{{f}}{m}\left( \cos \psi \sin \theta \cos \phi +\sin \psi \sin \phi \right)\\ {\dot{v}}_y=-\frac{{f}}{m}\left( \sin \psi \sin \theta \cos \phi -\cos \psi \sin \phi \right)\\ {\dot{v}}_z={g}-\frac{{f}}{m}\cos \phi \cos \theta\\ \end{cases}
(7)
这就得到了动力学模型中关于合外力和速度的方程,即位置动力学模型。接下来是关于合力矩和角速度的方程——姿态动力学模型。
2. 姿态动力学模型
由欧拉方程(2)可得:
\boldsymbol{J\dot{\omega}}^b+\boldsymbol{\omega }^b\times \boldsymbol{J\omega }^b=\boldsymbol{G}_{\boldsymbol{a}}+\boldsymbol{\tau } (8)
式中, \boldsymbol{\omega }^b 表示在机体坐标系下的角速度; \boldsymbol{G}_{\boldsymbol{a}} 表示陀螺力矩; \boldsymbol{\tau } 表示螺旋桨在机体轴上产生的力矩,包括绕 O_bx_b 轴的滚转力矩 {\tau }_x 、绕 O_by_b 轴的俯仰力矩 {\tau }_y 以及绕 O_bz_b 轴的偏航力矩 {\tau }_z 。
关于角速度 \boldsymbol{\omega }^b :为方便表示,分别用 p, q, r 来表示 \boldsymbol{\omega }^b 在机体轴上的三个分量: \omega_x, \omega_y, \omega_z ,即:
\boldsymbol{\omega }^b=\left[ \begin{array}{c} \omega _{xb}\\ \omega _{yb}\\ \omega _{zb}\\ \end{array} \right] =\left[ \begin{array}{c} p\\ q\\ r\\ \end{array} \right] (9)
关于陀螺力矩 \boldsymbol{G}_{\boldsymbol{a}} :当电机高速旋转的时候,相当于一个陀螺。高速旋转的陀螺是非常稳定的个体,具有保持自身轴向不变的能力。因此如果有外力想改变陀螺转轴的方向,那么会产生一个陀螺力矩来抵抗这种改变。这里直接给出 \boldsymbol{G}_{\boldsymbol{a}} 的计算公式:
\boldsymbol{G}_{\boldsymbol{a}}=\left[ \begin{array}{c} G_{a,\phi}\\ G_{a,\theta}\\ G_{a,\psi}\\ \end{array} \right] =\left[ \begin{array}{c} J_{RP}q\left( \varpi _1-\varpi _2+\varpi _3-\varpi _4 \right)\\ J_{RP}p\left( -\varpi _1+\varpi _2-\varpi _3+\varpi _4 \right)\\ 0\\ \end{array} \right] (10)
式中, J_{RP} 表示整个电机转子和螺旋桨绕机体转轴的总转动惯量; \varpi _1, \varpi _2, \varpi _3, \varpi _4 表示螺旋桨1,2,3,4的转速。关于陀螺力矩的详细推导可以参考下面这篇文章:
关于惯性矩阵 \boldsymbol{J} :基于假设1和假设2,惯性矩阵可表示为:
\boldsymbol{J}=\left[ \begin{matrix} J_{xx}& & \\ & J_{yy}& \\ & & J_{zz}\\ \end{matrix} \right] (11)
现在将式(9-11)代入到式(8)中,移项整理后得到:
\left[ \begin{array}{c} I_{xx}\dot{p}\\ I_{yy}\dot{q}\\ I_{zz}\dot{r}\\ \end{array} \right] =\left[ \begin{array}{c} qr\left( I_{yy}-I_{zz} \right)\\ pr\left( I_{zz}-I_{xx} \right)\\ pq\left( I_{xx}-I_{yy} \right)\\ \end{array} \right] +\left[ \begin{array}{c} -J_{RP}q\varOmega\\ J_{RP}p\varOmega\\ 0\\ \end{array} \right] +\left[ \begin{array}{c} \tau _x\\ \tau _y\\ \tau _z\\ \end{array} \right] \\ \Downarrow \\ \begin{cases} \dot{p}=\frac{1}{I_{xx}}\left[ \tau _x+qr\left( I_{yy}-I_{zz} \right) -J_{RP}q\varOmega \right]\\ \dot{q}=\frac{1}{I_{yy}}\left[ \tau _y+pr\left( I_{zz}-I_{xx} \right) +J_{RP}p\varOmega \right]\\ \dot{r}=\frac{1}{I_{zz}}\left[ \tau _z+pq\left( I_{xx}-I_{yy} \right) \right]\\ \end{cases}
(12)
式中, \varOmega =-\varpi _1+\varpi _2-\varpi _3+\varpi _4 。
至此,四旋翼飞行器的动力学模型建立完成。
八、四旋翼飞行器的运动学模型
运动学模型的输入为速度和角速度,输出为位置和姿态。
关于位置的方程比较简单,即:
\boldsymbol{\dot{p}}^e=\boldsymbol{v}^e (13)
式中, \boldsymbol{{p}}^e=\left[ \begin{matrix} x& y& z\\ \end{matrix} \right] ^T ,用来表示飞行器在地球坐标系中的坐标位置,展开后得:
\left[ \begin{matrix} \dot{x}& \dot{y}& \dot{z}\\ \end{matrix} \right] ^T=\left[ \begin{matrix} v_x& v_y& v_z\\ \end{matrix} \right] ^T (14)
接下来是关于姿态的方程。
表示姿态的方法有三种:欧拉角、旋转矩阵、四元数。本文只介绍欧拉角的表示方法。
姿态角的变化率与机体的旋转角速度有如下的关系:
\boldsymbol{\dot{\varTheta}}=\boldsymbol{W}\cdot \boldsymbol{\omega }^b (15)
式中, \boldsymbol{\varTheta } 为四旋翼的三个姿态角(欧拉角),且有:
\boldsymbol{\dot{\varTheta}}=\left[ \begin{matrix} \dot{\phi}& \dot{\theta}& \dot{\psi}\\ \end{matrix} \right] ^T , \boldsymbol{\omega }^b=\left[ \begin{matrix} \omega _{xb}& \omega _{yb}& \omega _{zb}\\ \end{matrix} \right] ^T=\left[ \begin{matrix} p& q& r\\ \end{matrix} \right] ^T
\boldsymbol{W}=\left[ \begin{matrix} 1& \tan \theta \sin \phi& \tan \theta \cos \phi\\ 0& \cos \phi& -\sin \phi\\ 0& \sin \phi /\cos \theta& \cos \phi /\cos \theta\\ \end{matrix} \right]
即:
\left[ \begin{array}{c} \dot{\phi}\\ \dot{\theta}\\ \dot{\psi}\\ \end{array} \right] =\left[ \begin{matrix} 1& \tan \theta \sin \phi& \tan \theta \cos \phi\\ 0& \cos \phi& -\sin \phi\\ 0& \sin \phi /\cos \theta& \cos \phi /\cos \theta\\ \end{matrix} \right] \left[ \begin{array}{c} p\\ q\\ r\\ \end{array} \right] (16)
关于姿态角的变化率与机体的旋转角速度为何不相等的解释以及推导过程可以参考下面两篇文章:
在小扰动的情况下,即各个角度的变化较小的前提下,姿态角的变化率与机体的旋转角速度近似相等,则有:
\left[ \begin{array}{c} \dot{\phi}\\ \dot{\theta}\\ \dot{\psi}\\ \end{array} \right] =\left[ \begin{array}{c} p\\ q\\ r\\ \end{array} \right] (17)
至此,四旋翼飞行器的运动学模型建立完成。
九、四旋翼飞行器的飞行控制刚体模型
四旋翼飞行器的飞行控制刚体模型由动力学模型和运动学模型结合而成。
将式(7)与式(14)结合,得到以下方程组:
\begin{cases} \ddot{x}=-\frac{f}{m}\left( \cos \psi \sin \theta \cos \phi +\sin \psi \sin \phi \right)\\ \ddot{y}=-\frac{f}{m}\left( \sin \psi \sin \theta \cos \phi -\cos \psi \sin \phi \right)\\ \ddot{z}=g-\frac{f}{m}\cos \phi \cos \theta\\ \end{cases} (18)
在小扰动的前提下,将式(12)与式(17)结合,得到以下方程组:
\begin{cases} \ddot{\phi}=\frac{1}{I_{xx}}\left[ \tau _x+qr\left( I_{yy}-I_{zz} \right) -J_{RP}q\varOmega \right]\\ \ddot{\theta}=\frac{1}{I_{yy}}\left[ \tau _y+pr\left( I_{zz}-I_{xx} \right) +J_{RP}p\varOmega \right]\\ \ddot{\psi}=\frac{1}{I_{zz}}\left[ \tau _z+pq\left( I_{xx}-I_{yy} \right) \right]\\ \end{cases} (19)
将式(18)与式(19)组合在一起,并使: \left[ \begin{matrix} U_1& U_2& U_3& U_4\\ \end{matrix} \right] ^T=\left[ \begin{matrix} f& \tau _x& \tau _y& \tau _z\\ \end{matrix} \right] ^T (动力学模型的输入量,与螺旋桨转速的平方成线性关系),即可得到四旋翼飞行器的非线性六自由度模型:
\begin{cases} \ddot{x}=-\frac{U_1}{m}\left( \cos \psi \sin \theta \cos \phi +\sin \psi \sin \phi \right)\\ \ddot{y}=-\frac{U_1}{m}\left( \sin \psi \sin \theta \cos \phi -\cos \psi \sin \phi \right)\\ \ddot{z}=g-\frac{U_1}{m}\cos \phi \cos \theta\\ \begin{array}{l} \ddot{\phi}=\frac{1}{I_{xx}}\left[ U_2+qr\left( I_{yy}-I_{zz} \right) -J_{RP}q\varOmega \right]\\ \ddot{\theta}=\frac{1}{I_{yy}}\left[ U_3+pr\left( I_{zz}-I_{xx} \right) +J_{RP}p\varOmega \right]\\ \ddot{\psi}=\frac{1}{I_{zz}}\left[ U_4+pq\left( I_{xx}-I_{yy} \right) \right]\\ \end{array}\\ \end{cases} (20)
也可以将式(6)、式(8)、式(13)、式(15)联合起来得到以下方程组:
\begin{cases} \boldsymbol{\dot{p}}^e=\boldsymbol{v}^e\\ \boldsymbol{\dot{v}}^e=g\boldsymbol{e}_3-\frac{f}{m}\boldsymbol{R}_{b}^{e}\boldsymbol{e}_3\\ \boldsymbol{\dot{\varTheta}}=\boldsymbol{W}\cdot \boldsymbol{\omega }^b\\ \boldsymbol{J\dot{\omega}}^b=-\boldsymbol{\omega }^b\times \boldsymbol{J\omega }^b+\boldsymbol{G}_{\boldsymbol{a}}+\boldsymbol{\tau }\\ \end{cases} (21)
十、结语
- 下一步将给出四旋翼飞行器的控制效率模型;
- 四旋翼飞行器的飞行控制刚体模型建立起来后,便可以根据此模型设计控制器。
——2021.02.05
参考
- ^abc全权. 多旋翼飞行器设计与控制[M]. 北京: 电子工业出版社, 2018.
- ^MAHONY R, KUMAR V, CORKE P. Multirotor Aerial Vehicles: Modeling, Estimation, and Control of Quadrotor[J]. IEEE robotics & automation magazine, 2012,19(3): 20-32.
|
|