基于FFT的柯林斯衍射公式的数值计算

径向加速度

前言：

近轴光学系统的衍射计算是光学专业的重要模块，但是对于多组件的复杂光学系统的衍射计算，如果逐组件地去做衍射积分，听起来就非常繁琐和复杂，还会面临重采样等问题。
如果有一种简洁的计算方法，对复杂近轴光学系统通过一次衍射积分就可以实现仿真计算，那听起来挺还不错的对吧。
这个方法就是柯林斯公式（Collins' formula）。
通过一个等效ABCD矩阵来表示复杂近轴光学系统，然后基于ABCD系数，按柯林斯公式进行一次衍射积分计算，即可完成对复杂光学系统的衍射仿真。这在全息显示、光束整形、光场调控等领域都有广泛的应用。
本文内容主要是介绍如何基于Matlab中的FFT完成柯林斯公式的数值计算，以及数值计算中的一些重要细节。
（*在本科学弟的指点下，本人对此问题终于略有小得 ，在这里把一点成果和体会做个整理记录）
本文抛砖引玉，疏误之处，万望不吝指正！
1、近轴光学系统和ABCD矩阵法

每个工具或者理论，使用之前一定搞清楚其适用范围，本文所述的方法仅限于近轴光学系统。
所谓近轴光学系统，就是指孔径角θ的光学系统，在这个近轴条件的限定下，可以有如下近似：
sinθ=θ \\这个近似非常重要，因为几何光学中光线、光轴以及像高等参数之间的分析离不开三角函数，但是三角函数是难以计算求解的，因此一般把三角函数展开为多项式来表达，但是冗长的高阶表达式会使得计算分析非常复杂（参考像差理论的分析）。然而在近轴条件的近似之下，令sinθ=θ，就可以不予考虑sin展开式后面冗长的高阶项，大大简化光学系统的表示、分析和计算。

基于近轴条件，每根光线只需要两个量来表示，即离轴坐标X和孔径角θ（光线和光轴的夹角），例如下图中入射和出射光线就可以分别表示为：
\begin{bmatrix} x2\\θ2\end{bmatrix} , \begin{bmatrix} x2\\θ2\end{bmatrix} \\



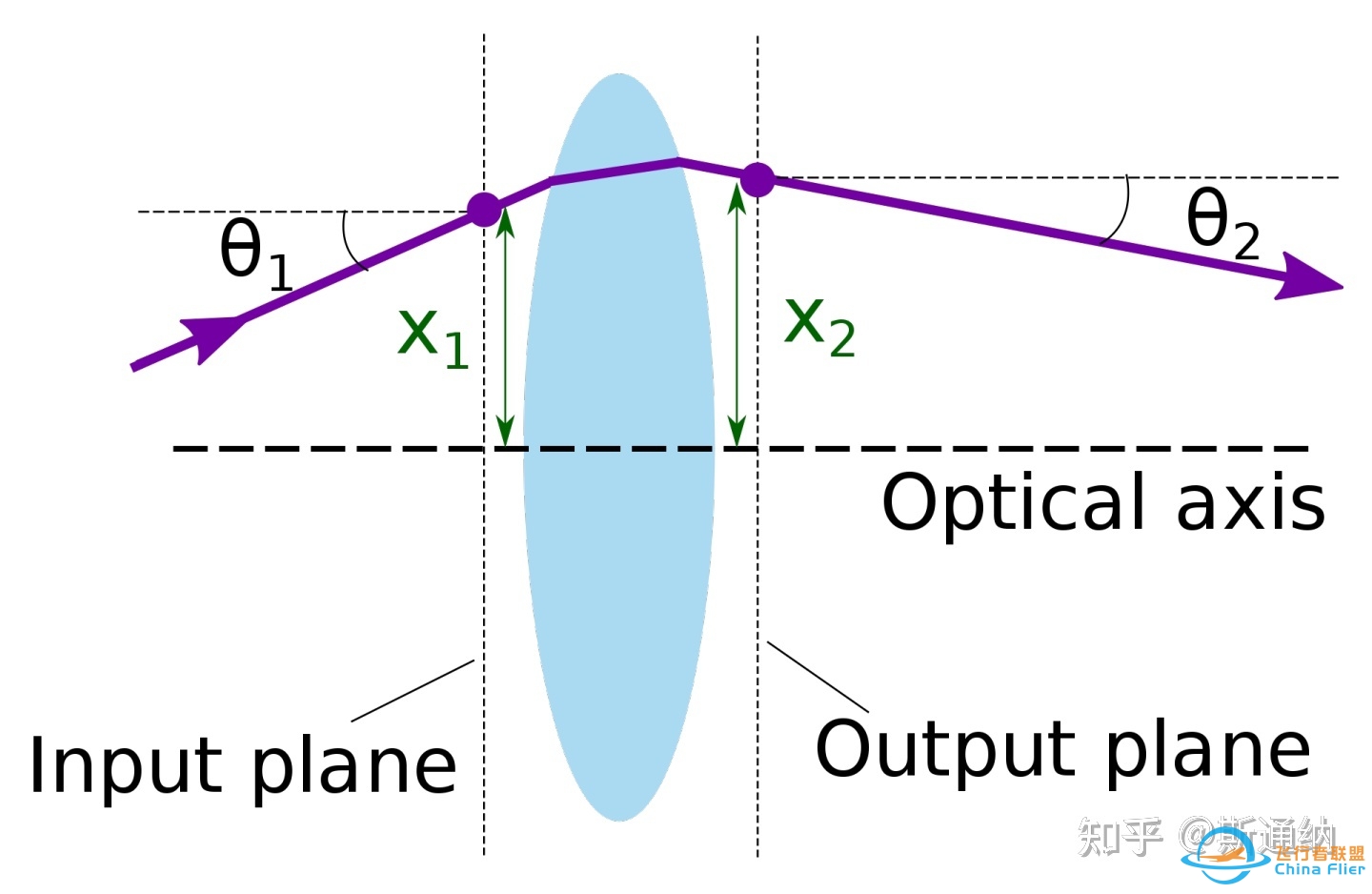
Wikipedia

因此任意光学元件对于光线的作用即可以通过一个2*2的光线传输矩阵来实现，这就是所谓的ABCD矩阵，具体表现形式如下：
\begin{bmatrix} x2\\θ2\end{bmatrix} = \begin{bmatrix} A&B\\C&D\end{bmatrix} \begin{bmatrix} x1\\θ1\end{bmatrix} \\ 下图展示了近轴光学系统中常见组件的ABCD矩阵。



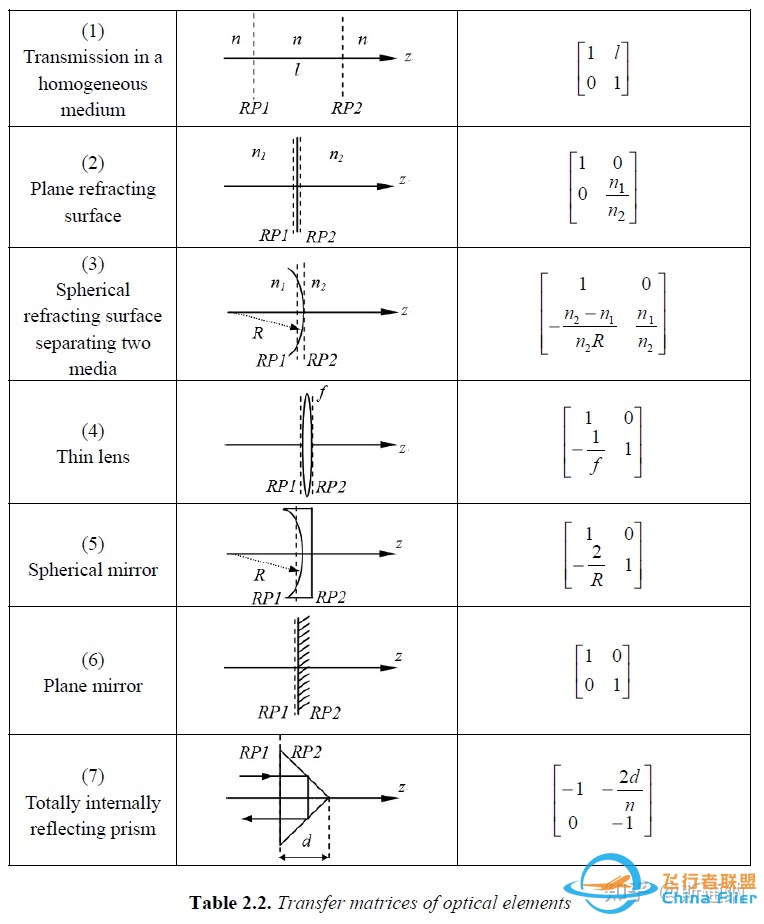
Picart P, Li J. Digital holography[M]. John Wiley & Sons, 2013.

对于一个多组件的复杂光学系统，以一个单透镜成像系统为例，



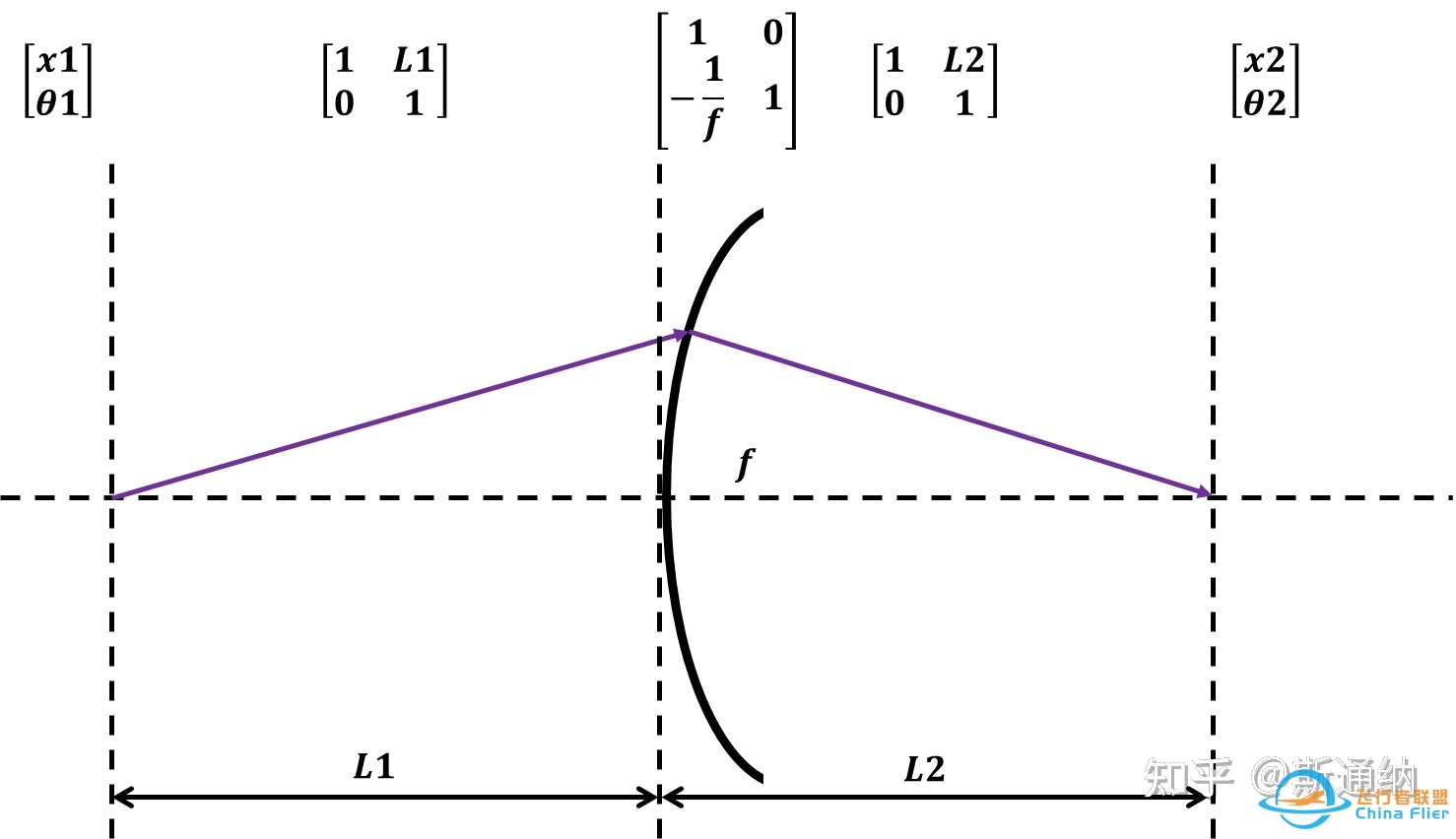
本人PPT手绘，疏漏之处敬请指正

\begin{bmatrix} x2\\θ2\end{bmatrix} = \begin{bmatrix} 1&L2\\0&1\end{bmatrix}\begin{bmatrix} 1&0\\-1/f&1\end{bmatrix} \begin{bmatrix} 1&L1\\0&1\end{bmatrix}  \begin{bmatrix} x1\\θ1\end{bmatrix} \\那么这个多组件光学系统的可以等效成一个ABCD矩阵：
\begin{bmatrix} A&B\\C&D\end{bmatrix} = \begin{bmatrix} 1&L2\\0&1\end{bmatrix}\begin{bmatrix} 1&0\\-1/f&1\end{bmatrix} \begin{bmatrix} 1&L1\\0&1\end{bmatrix} \\
为什么这样画一个多组件光学系统呢，一方面是因为后面还会用这个系统做示例，可以复用，另一方面是为了展示强调一个重要点，就是等效矩阵的计算的顺序，越靠近入射光的组件，越放在右边。
这一点在实践中经常被疏忽，一般光学系统画图是从左往右传播，往往计算等效ABCD矩阵时便下意识的从左往右依次计算，最后导致错误的结果。
2、柯林斯公式及其基于快速傅里叶变换的实现

经过上一节的介绍，我们终于可以进入正题了。
我们已经知道，对于任一常见近轴光学系统，我们都可以用一个ABCD矩阵来等效表示，那么对应系统的衍射计算，是否可以仅基于此等效ABCD矩阵来实现呢？柯林斯公式给出了肯定的答案。
2.1、简介柯林斯公式




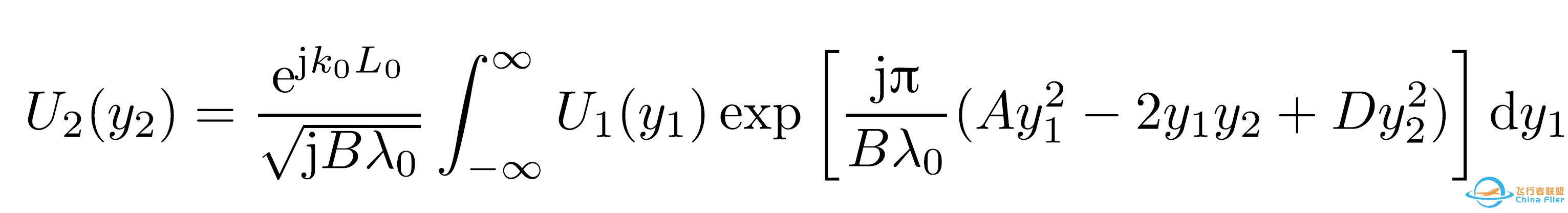
一维公式, Introduction to Fourier Optics 4th edition, Goodman



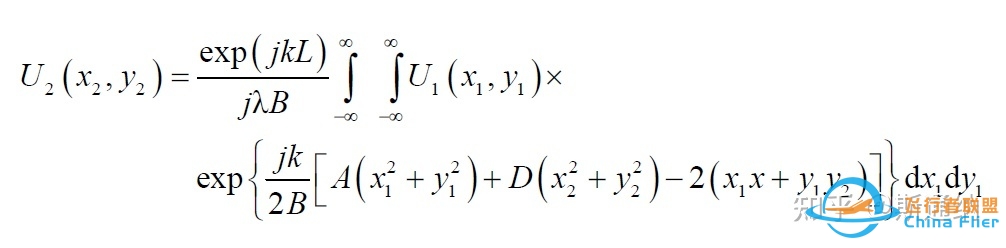
二维公式，Digital holography. Picart P, Li J.

本文仅就一维公式为例分析，二维公式可以参考一维自行推理。
对一维公式中相关参数做说明，
A，B，C，D 即是光线传输矩阵的四个元素。
U1(y1) 是输入光场， y1 是入射平面的空间坐标， U2(y2) 是输出光场，y2 是出射平面的空间坐标。
\lambda0 是波长，波矢 k0=2\pi/\lambda0。
额外需要注意的是这个 L0，其代表整个近轴光学系统从入射面到出射面沿光轴累计的总长度。以第一节中所示的单个薄透镜的成像系统为例，此系统沿光轴总长L0=L1+L2。
2.2、柯林斯公式与傅里叶变换

我们对2.1所示柯林斯公式的形式做一点小的调整，即把指数项分立开，将积分无关项提出积分外，：
U_2(y_2)=\frac{e^{jk_0L_0}}{\sqrt{jB\lambda_0}}\cdot e^{\frac{j\pi D}{B\lambda_0}y_2^{2}}\cdot\int_{-\infty}^{\infty}{U_1(y_1)\cdot e^{\frac{j\pi A}{B\lambda_0}y_1^{2}}\cdot e^{\frac{j2\pi y_2}{B\lambda_0}y_1} }dy_1 \\ 这个公式中，积分部分的形式是否有一点熟悉，我们令积分部分结果等于中间量 U'_2
U'_2(\frac{y_2}{B\lambda_0})=\int_{-\infty}^{\infty}{[U_1(y_1)\cdot e^{\frac{j\pi A}{B\lambda_0}y_1^{2}}]\cdot e^{\frac{j2\pi y_2}{B\lambda_0}y_1} }dy_1 \\如果令  f=\frac{y_2}{B\lambda_0}  （这个等式是关键！重要等式，后面我们会对这个做一个分析）
让我们翻出本科教材，看一下傅里叶变换的公式：
X(f)=\int_{-\infty}^{\infty}{x(t)\cdot e^{-j2\pi f t} }dt = F  [x(t)]\\
不能说很像，只能说是一模一样（* F[x(t)] 代表对 x(t) 做傅里叶变换）
所以整个柯林斯公式可以写成，其中 f=\frac{y_2}{B\lambda_0}  ：
U_2(f)=\frac{e^{jk_0L_0}}{\sqrt{jB\lambda_0}}\cdot e^{\frac{j\pi D}{B\lambda_0}y_2^{2}}\cdot\int_{-\infty}^{\infty}{[U_1(y_1)\cdot e^{\frac{j\pi A}{B\lambda_0}y_1^{2}}]\cdot e^{j2\pi fy_1} }dy_1 \\=\frac{e^{jk_0L_0}}{\sqrt{jB\lambda_0}}\cdot e^{\frac{j\pi D}{B\lambda_0}y_2^{2}}\cdot F[U_1(y_1)\cdot e^{\frac{j\pi A}{B\lambda_0}y_1^{2}}] \\
由此可得，我们可以将柯林斯公式的衍射积分基于傅里叶变换来实现。
Note：输出面频域坐标的具体取值方式
关于上述的重要等式 f=\frac{y_2}{B\lambda_0} ，这里我也想就此关于做一个小辨析。因为光学衍射可以通过傅里叶变换来实现，因此我们也经常将衍射的输入面和输出面成为空间域和频域，但是关于频域的坐标取值，其实经常会因为概念不清淅发生混淆，尤其是你想对衍射公式做数值实现经常造成混淆。



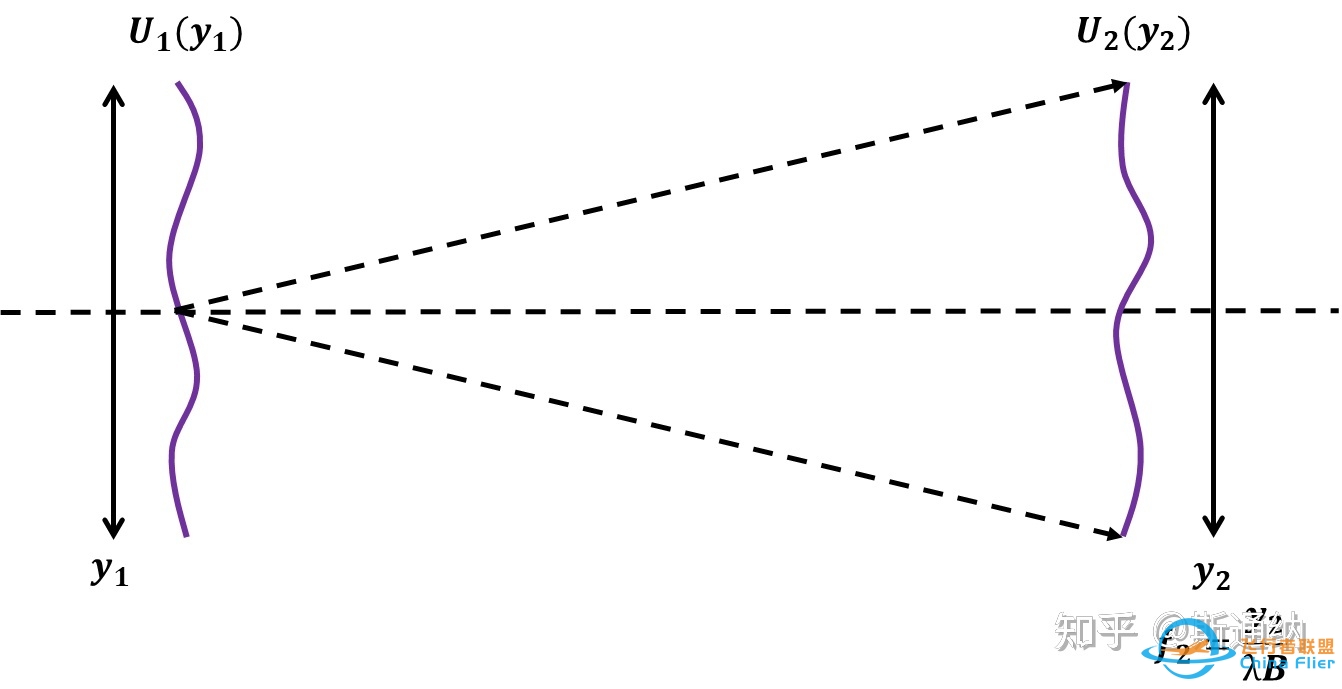
本人PPT手绘

输入平面，称之为空间域，采样点的坐标按 y_1 来取，是没问题的。
输出平面，称之为频域，那么频域的坐标点可以是按 y_2 来取吗？答案是否定的。
输出平面的信号是一个一维或者二维的衍射图，衍射图每个点的空间位置自然是 y_2 空间坐标，但是在衍射计算的傅里叶变换公式中，将 y_2 直接视为输出面的频域坐标是不对的。
因为我们将衍射公式等效成傅里叶变换公式，等效等式是 f=\frac{y_2}{B\lambda_0}  ，因此频域的坐标值是这个 f ，而不能直接用 y_2 。
2.3、从傅里叶变换到离散傅里叶变换

为了数值计算的方便，我们需要将连续的傅里叶变换变成离散傅里叶变换。
为了从我们熟悉的信号系统的角度的思维方便，我们将输入光场的空间域 y_1 称为时域，将变换之后的输出光场的空间域 y2 按等效式 f=\frac{y_2}{B\lambda_0} 来看称为频域。
关于一些概念的简单辨析：

有限和无限长度：傅里叶变换对应的信号都是无限长度的， 我们所说的有限长信号，就是指在有限长度内显式的指定了值，而在其余位置都默认是0。

周期和非周期：非周期信号的长度可以是无限也可以是有限的，因为在无限长度内都有值，但是没有周期性，或者只在一段区域有值，其余位置都是0，都可以被称为非周期信号。但是周期信号一定是无限长且保持周期性的。

离散和非离散：离散信号的值，只取在固定位置或坐标下，连续信号就是在任意位置都有值。数学表达式能表示连续的信号，但是计算机处理的都是离散的信号，因为都是一串具体位置的值。

*一些比较粗糙的理解，请批判。

通过翻阅本科教材信号与线性系统，可以得到下述的两组公式对。
1、傅里叶 变换\逆变换 公式对，其中 w=2\pi f ：
F(jw)=\int_{-\infty}^{\infty}f(t)e^{-jwt}dt \\
f(t)=\frac{1}{2\pi}\int_{-\infty}^{\infty}F(jw)e^{jwt}dw \\
2、离散傅里叶 变换\逆变换 公式对， 其中W_N^{mk}=e^{-j\frac{2\pi }{N}mk} ：
F[m]=DFT\{f[k]\}=\sum_{k=0}^{N-1} f[k]\cdot W_N^{mk}~~,~~    (m=0,1,···,N-1)  \\f[k]=IDFT\{F[m]\}=\frac{1}{N}\sum_{m=0}^{N-1} F[m]\cdot W_N^{-mk}   ~~,~~    (k=0,1,···,N-1)  \\
这里需要重视傅里叶变换的一个重要性质：时域离散，则频域周期；时域周期，则频域离散。
举例来看说明“时域周期<—>频域离散”，因为频域每一个离散的脉冲值，都对应时域一个无限长的周期信号，因此频域若干离散脉冲值，对应时域信号是若干个无限长周期信号的叠加，依旧是无限长的周期信号。
但是我们数值计算的时候，时域和频域的点都需要是离散的，这就要求时域和频域信号都是周期无限长的，但是我们采集和计算的信号都是有限长度的。
这里只需要用一个小trick，那就是将采集到的有限长信号，默认周期延拓到无限长度即可。这样就两全其美了。
时域信号，离散，周期无限长；对应频域信号，周期无限长，离散。
我们到手处理的就是下图中红色区域的有限长度的离散信号，但是实际上是默认周期延拓。



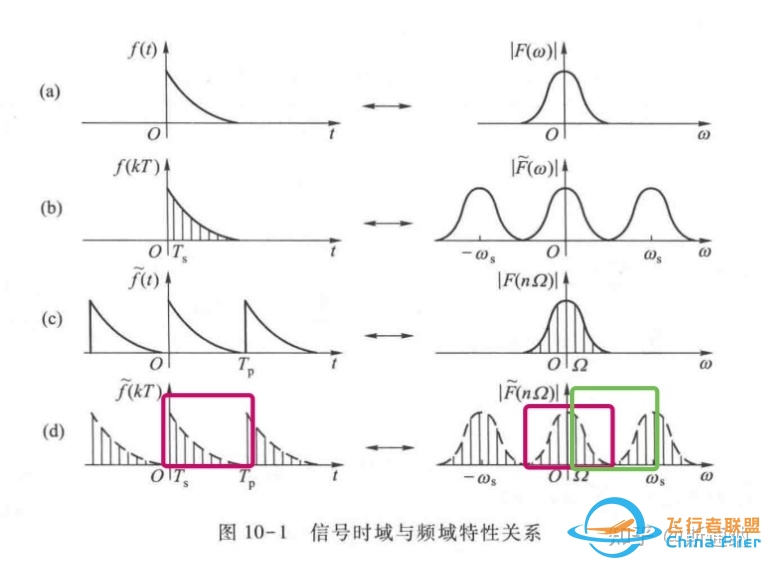
信号与线性系统，管致中，夏恭恪，孟桥

通过下图，我们能了解从傅里叶变换到离散傅里叶变换的更详细的过程。




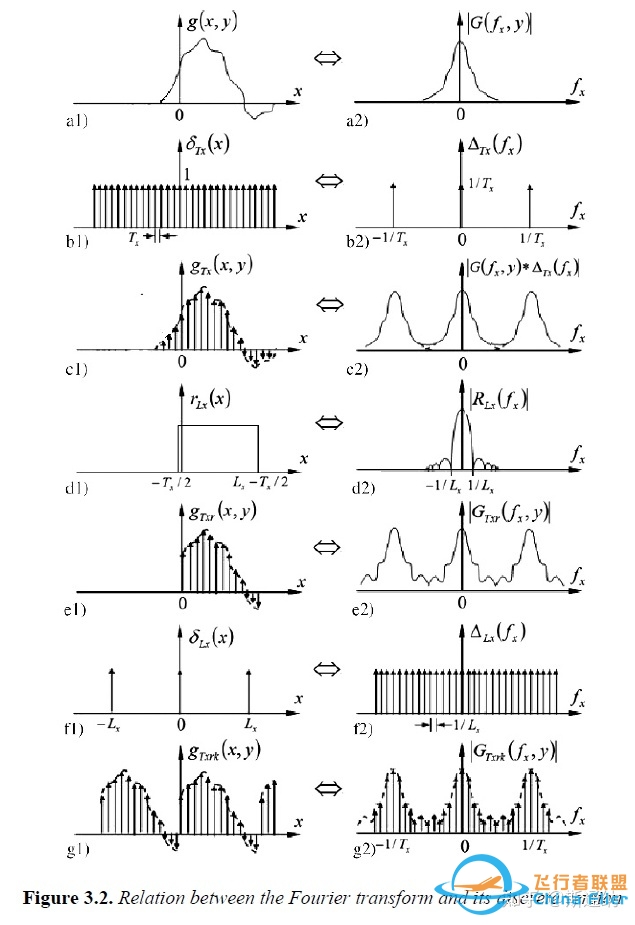
Digital holography. Picart P, Li J.

2.4、基于FFT的柯林斯公式整理

基于上述几节的内容，我们已经可以将柯林斯公式整理成基于DFT实现的形式：
U_2(f)=\frac{e^{jk_0L_0}}{\sqrt{jB\lambda_0}}\cdot e^{\frac{j\pi D}{B\lambda_0}y_2^{2}}\cdot\int_{-\infty}^{\infty}{[U_1(y_1)\cdot e^{\frac{j\pi A}{B\lambda_0}y_1^{2}}]\cdot e^{-j2\pi fy_1} }dy_1 \\=\frac{e^{jk_0L_0}}{\sqrt{jB\lambda_0}}\cdot e^{\frac{j\pi D}{B\lambda_0}y_2^{2}}\cdot F[U_1(y_1)\cdot e^{\frac{j\pi A}{B\lambda_0}y_1^{2}}] \\ =\frac{e^{jk_0L_0}}{\sqrt{jB\lambda_0}}\cdot e^{\frac{j\pi D}{B\lambda_0}y_2^{2}}\cdot DFT[U_1(y_1)\cdot e^{\frac{j\pi A}{B\lambda_0}y_1^{2}}] \\ =\frac{e^{jk_0L_0}}{\sqrt{jB\lambda_0}}\cdot e^{\frac{j\pi D}{B\lambda_0}y_2^{2}}\cdot FFT[U_1(y_1)\cdot e^{\frac{j\pi A}{B\lambda_0}y_1^{2}}] \\因此我们仅仅需要通过DFT来计算入射光场，然后乘上外面的积分无关项即可。
而FFT是DFT的一种快速算法，我们基于FFT就可以很容易实现柯林斯公式的数值计算。
看起来胜利曙光就在眼前，但是往往黎明前最黑暗。
上面的内容基本就是参考教科书的公式，将其堆叠起来，建立一些必要的基础知识和理解。但是里最后的实现依旧还是有一段比较曲折的路要走。
下面第三章会对实践中到若干关键细节问题做辨析及处理，这一章也是本帖的精华所在。
2.5、物象共轭点的特殊情况

如果输入输出光场位置恰巧位于光学系统的物像共轭点，例 \frac{1}{f}=\frac{1}{L_1}+\frac{1}{L_2} ，则ABCD矩阵中B的值为0。
这时就不能直接套用柯林斯公式，而应该用下述公式，
U_2(y_2)=\frac{e^{jkL_0}}{\sqrt{A}} \cdot exp(\frac{j\pi C y_2^2}{\lambda A}) \cdot U_1(\frac{y_2}{A}) \\
3、衍射数值计算中需要考虑的若干细节

即使知道了理论公式，在真正编程实现衍射计算大家依旧会面临很多问题，尤其是采样和坐标值的问题。这章就会对这些比较关键的问题做一些辨析和补充。
3.1、适应衍射计算的离散傅里叶变换公式

通过比较信号系统教材上的傅里叶变换公式和离散傅里叶变换公式：
傅里叶变换，其中 w=2\pi f ：
F(jw)=\int_{-\infty}^{\infty}f(t)e^{-jwt}dt \\
离散傅里叶变换， 其中W_N^{mk}=e^{-j\frac{2\pi }{N}mk} ：
F[m]=DFT\{f[k]\}=\sum_{k=0}^{N-1} f[k]\cdot W_N^{mk}~~,~~    (m=0,1,···,N-1)  \\
从傅里叶变换到离散傅里叶变换，实际上就是将连续积分公式变成了数值离散求和公式。
我提供一个视角，即，连续函数的傅里叶变换中，信号的采样间隔是dt，是一个无穷小量，而在离散傅里叶变换中，信号的采样间隔Δt=1以及Δf=1，且将积分符号也换成了求和符号。
因为采样间隔因为默认是1，就将其忽略了。但是在光学数值计算中，采样间隔并非固定是1，所以这里将离散积分公式重新写一下。
因此最终离散形式傅里叶变换公式应该这么写：
F[m\cdot\Delta f]=DFT\{f[k\cdot\Delta t]\}
~~~~~~~~~~~~~~~~~~=\sum_{k=0}^{N-1} f[k\cdot\Delta t]\cdot e^{-j\frac{2\pi }{N\cdot \Delta t}(m\cdot\Delta f) (k\cdot\Delta t)}\cdot \Delta t~~,~~ (m=0,1,···,N-1)   
我们常用FFT来对输入序列做DFT，他是不考虑输入和输出的采样间隔的值的，因此实际上这个FFT只做了下图中红色方框中的部分，为了得到逼近连续傅里叶变换的准确值，需要在FFT输出的序列上乘上输入信号的采样间隔值 \Delta t 。


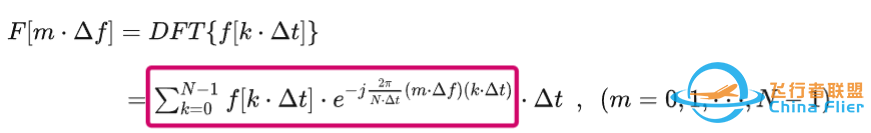
因此将完成柯林斯公式改成空间坐标的形式，令
输入平面，坐标y_1 的范围长度为 L_1，采样点数为 N_1 ，采样间隔为 \Delta y_1。
输出平面，坐标y_2 的范围长度为 L_2，采样点数为 N_2 ，采样间隔为 \Delta y_2；
对应频域点坐标f_2=\frac{y_2}{\lambda B} ，其范围长度为 \frac{L_2}{\lambda B}，采样点数为 N_2 ，采样间隔为 \frac{\Delta y_2}{\lambda B}。
因此科林斯公式写成：
U_2(f_2)=\frac{e^{jkL_1}}{\sqrt{jB\lambda}}\cdot e^{\frac{j\pi D}{B\lambda}y_2^{2}}\cdot\ FFT{[U_1(y_1)\cdot e^{\frac{j\pi A}{B\lambda}y_1^{2}}]\cdot } \Delta y_1 \\
3.2、fft与fftshift及对应坐标取值

Matlab中我们使用fft，为什么要同时要用fftshift？本节将对这问题做说明。
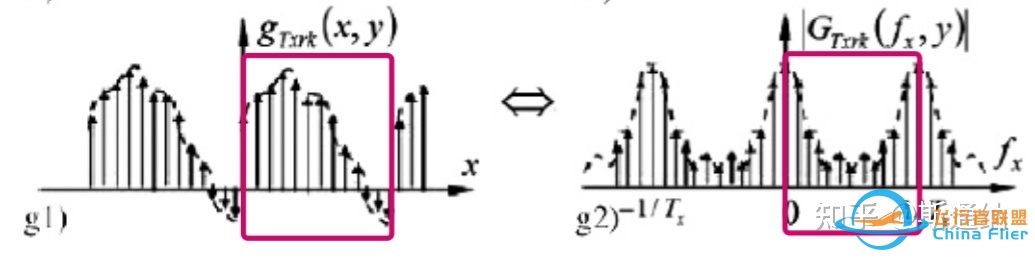
如前2.3节所述，我们做FFT变换，实际是无限周期的离散序列变换成无限周期的离散序列。
我们所需要那段信号序列，只是周期内的部分，如下图红色部分。


举例说明一下：


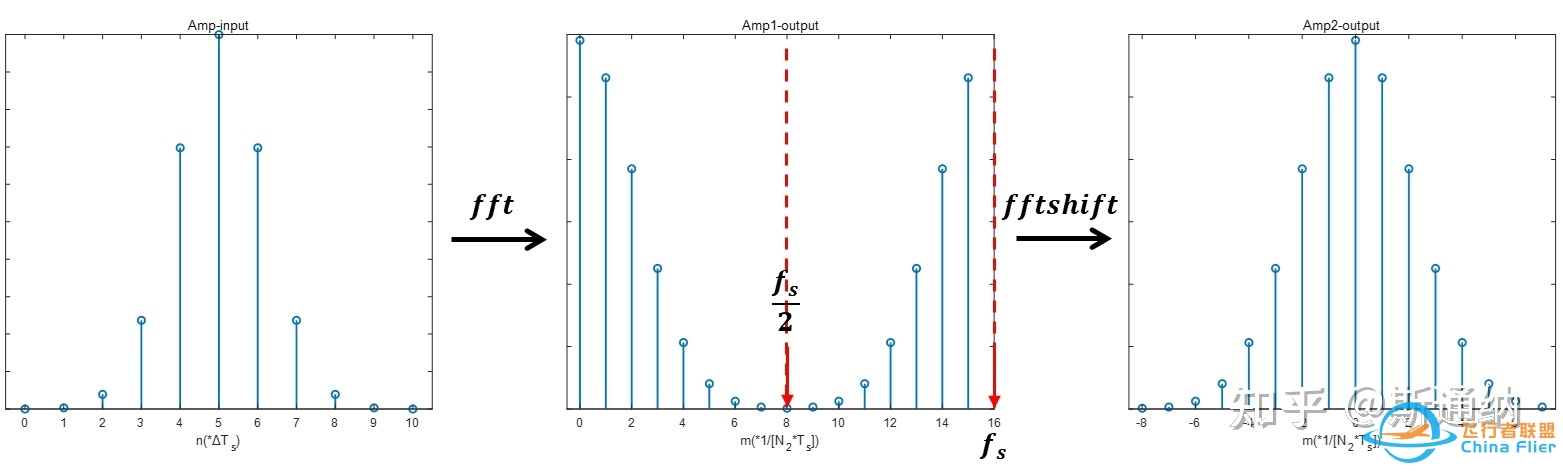
a、左图是输入信号，N_1=11，采样间隔 T_s ，采样频率f_s=\frac{1}{T_s}。
b、中图是fft输出信号【仅展示幅度谱】，设置fft的采样点数N_2=16 。
输出信号的频谱范围取决于输入的采样间隔， f_s=\frac{1}{T_s} ，而输出采样点数目是自己设置的 N_2 ,则输出信号的采样间隔 \Delta f=\frac{f_s}{N_2}=\frac{1}{Ts \cdot N_2} 。
c、右图是fftshift之后的信号，是通过对 0\sim f_s 范围内的信号，根据周期频谱的对称性，将左右半扇（【0~7】与【8~15】）进行对调，拼出0位置为中心的频谱信号。
注意fftshift之后，坐标序号的范围是【-8,-7, ... ,0, ... ,7】,共16个点，两端点的坐标值并非对称。
将序号用 N_2 来表示，乘上频谱采样间隔，则得到输出频谱真实的采样坐标 f=[-(\frac{N_2}{2}), ... ,(\frac{N_2}{2} -1)] \cdot \frac{1}{N_2\cdot T_s }\\
3.3、序列时移导致的线性相位补偿

一般我们的衍射计算都是中心的采样，但是我们常常发现这种采样方式，计算出来的光场会带有线性相位。
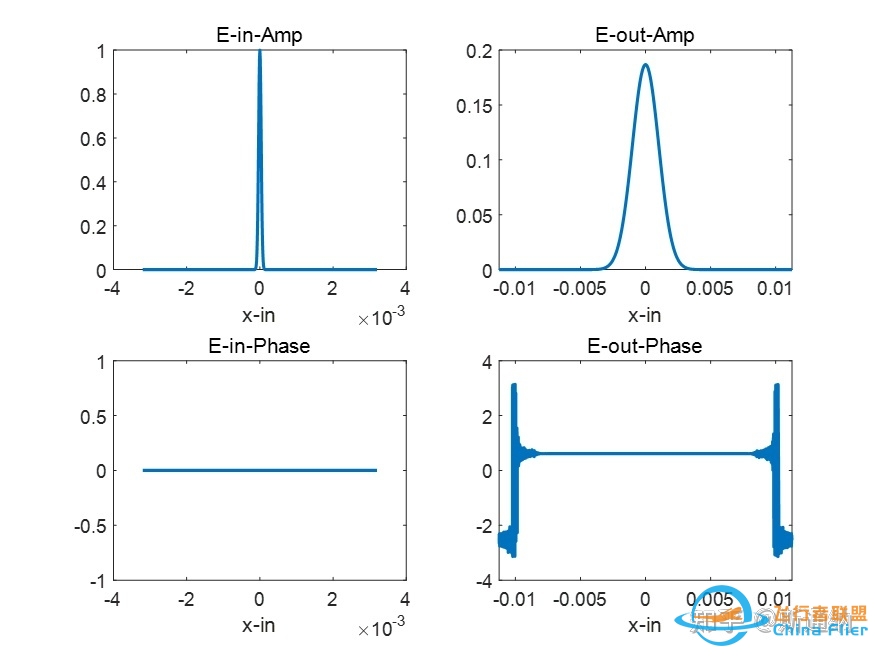
以高斯光束经过2f系统为例，2f系统，前焦面为光束束腰位置，理论上输出后焦面也应该是光束束腰，相位面为常数，但是直接仿真结果带有线性相位，这里不符我们的光学基础概念。



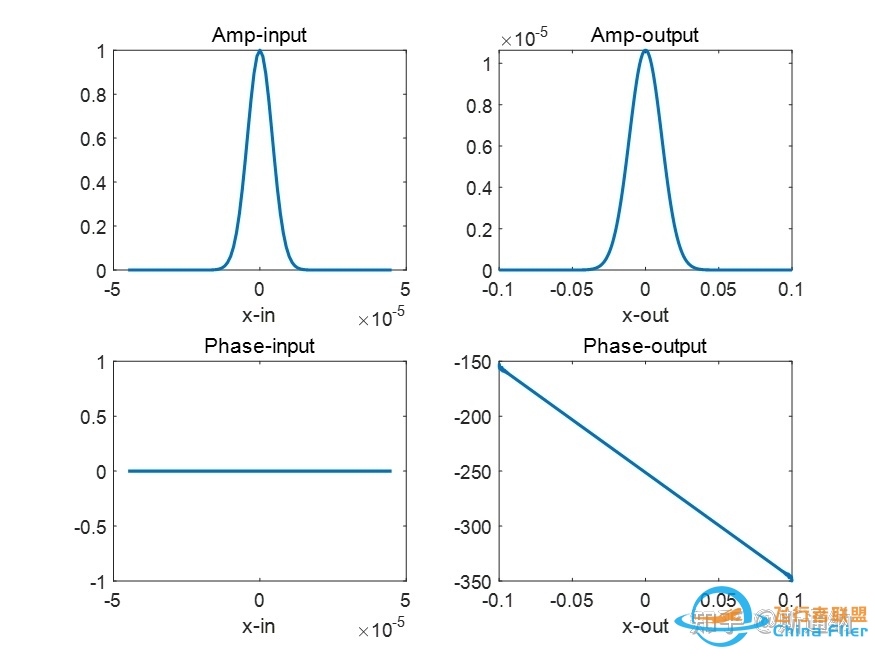
经过2f系统变换的输入输出光场的幅值及相位

实际上这可以用傅里叶变换的时移特性来解释。
若：f(t)\leftrightarrow  F(j\omega)\\
则： f(t-t_0)\leftrightarrow  F(j\omega)\cdot e^{-j\omega t_0}\\
我们期待输入的光场序列是这样的，（注意横坐标，是中心对称的）：


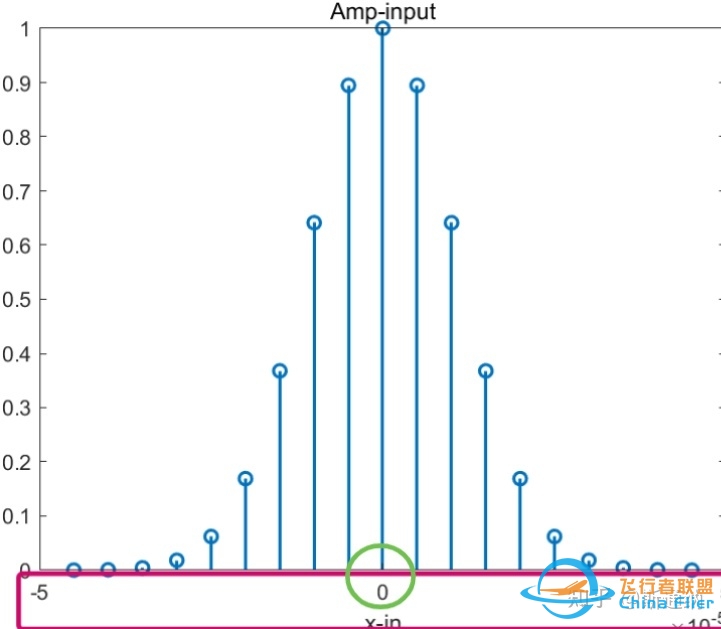
但是实际上，将这串光场采样值的序列输入到FFT算法中去，他默认是将其按首位在0位置开始计算的，如下图：


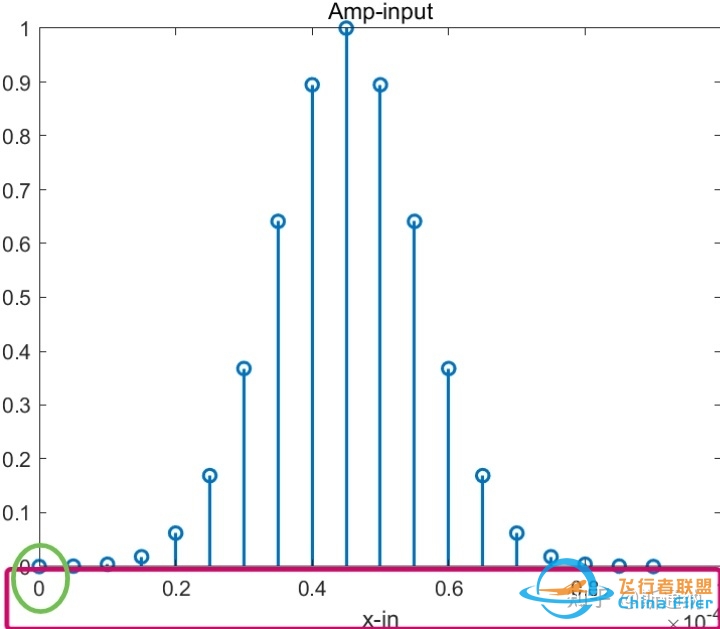
因此为了得到符合我们期待的中心对称的采样坐标的光场（移位主要是影响相位），还需要添加一个由于序列移位引入的线性相位补偿项，如下式最后一项：
U'_2=FFT[U'_1]*\Delta y_1 *e^{-j\cdot 2\pi \cdot f_2 \cdot (y_1[0])}\\ 式中 y_1[0] 即代表输入序列中第一位的坐标值。
4、数值计算代码

以高斯光束经过2f系统为例，编写代码图下：
clear
close all

%% 所有长度单位: 米/m

%%仿真参数
sampling_size =10e-6;
fft_sample=2^16;
xin = -3200e-6:sampling_size:3200e-6;
%% 输入光束属性
wavelength = 450e-9;
k=2*pi/wavelength;
w_f = (50e-6);%半径
E_amp = exp(-xin.^2/w_f^2);
E_phase = zeros(size(E_amp));
%% 光学系统参数
z1=0.5;
fT=0.5;
z2=0.5;

%% colins
%建立光学系统的ABCD矩阵
syms d1 d2 f
m1=[1 d1;0 1];
m2=[1 0;-1/f,1];
m3=[1,d2;0,1];
m=m3*m2*m1;
%%计算ABCD实际的值
d1=z1;
d2=z2;
f=fT;
z_axis=d1+d2;

ABCD=eval(m);
A=ABCD(1,1);
B=ABCD(1,2);
C=ABCD(2,1);
D=ABCD(2,2);

%% 输入\输出平面的定义
%input plane
%采样间距
dxin=mean(abs(diff(xin)));
%输入面坐标
xin;

%%输入场
%1、无调制
% E_in=E_amp.*exp(1j*E_phase);
%2、闪耀光栅相位调制
% E_phase_2=angle(exp(1i*0.002*k*xin));
% E_in=E_amp.*exp(1j*(E_phase+E_phase_2));
%3、二元光栅相位调制
% E_phase_2=floor((angle(exp(1i*0.005*k*xin))+pi)/pi)*pi;
% E_in=E_amp.*exp(1j*(E_phase+E_phase_2));
%3、矩形窗调幅
E_amp_2=double(abs(xin)<40e-6);
E_in=(E_amp.*E_amp_2).*exp(1j*(E_phase));

%%输入场绘图
figure(1)
subplot(2,2,1)
plot(xin,abs(E_in),'LineWidth',1.5)
title('E-in-Amp')
xlabel('x-in')
subplot(2,2,3)
plot(xin,angle(E_in),'LineWidth',1.5)
title('E-in-Phase')
xlabel('x-in')

if B==0 %% 共轭面情况
    x_out = x_in*A;
    dxout = mean(abs(diff(x_out)));
    E_out = E_in/sqrt(A).*exp(1i*pi*C/wavelength/A*x_out.^2);
else %% 非共轭面情况
    %% 输出平面的定义
    %output plane
    %平面边长
    Lout=wavelength*B/dxin;
    %采样间距
    dxout=Lout/(fft_sample);
    %输出面空间坐标
    x_out=((-fft_sample)/2:1:(fft_sample)/2-1)*dxout;%1/dxin/fft_sample;
    %输出面频域坐标
    fxout=((-fft_sample)/2:1:(fft_sample)/2-1)*1/dxin/fft_sample;%x_out/B/wavelength;
   
    %% 柯林斯公式衍射计算   
    E_in_temp=E_in.*exp(1j*pi*A/wavelength/B*x_in.^2);
    E_out_temp1=fftshift(fft(E_in_temp,fft_sample))*dxin;%fft计算
    E_out_temp2=E_out_temp1.*exp(-1i*2*pi*fxout*x_in(1));%线性相位补偿
    E_out=E_out_temp2.*exp(1j*k*D/2/B*x_out.^2).*exp(1j*k*z_axis)/sqrt(1j*wavelength*B);

end

%% 输出场绘图
subplot(2,2,2)
plot(x_out,abs(E_out),'LineWidth',1.5)
title('E-out-Amp')
xlabel('x-in')
subplot(2,2,4)
plot(x_out,phase(E_out),'LineWidth',1.5)
title('E-out-Phase')
xlabel('x-in')

%% 能量守恒验证
I_in=E_in*E_in'*dxin;
I_out=E_out*E_out'*dxout;
I_res=I_out-I_in;
5、衍射数值计算准确性的验证

衍射计算准确性验证，对于如下2f系统，对输入光场做相关定义，通过输出光场形貌验证是否准确。



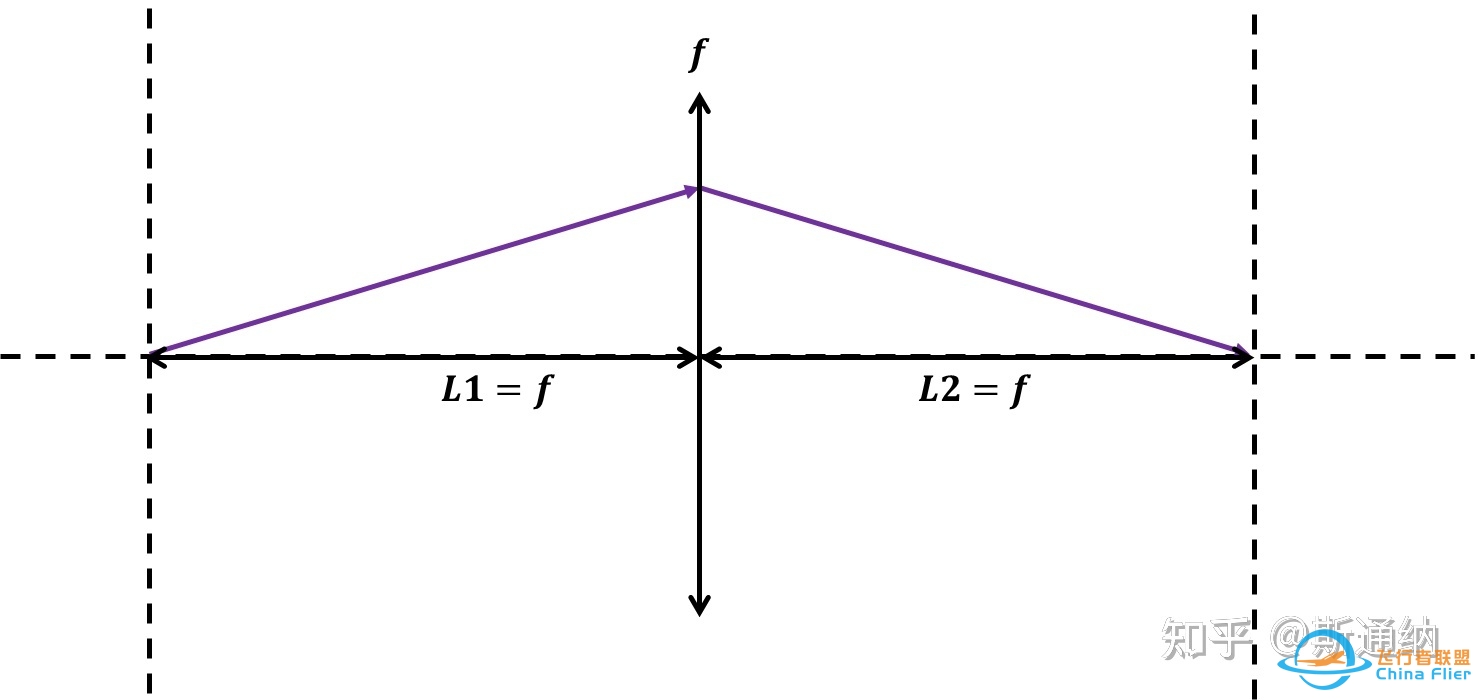
2f系统

1、相位形貌

输入位置为高斯光束束腰，输出光束应该也为高斯光束束腰，主要能量区域内相位面应为常数值。


2、幅度形貌

分别做如下调制，观察输出光束的幅度形貌是否符合常识。
a、闪耀光栅相位调制，输出高斯光束中心位置应该位移到+1衍射级位置；
b、二元光栅相位调制，输出应该分别有显著的两个+1、-1衍射级；
c、矩形窗幅度调制，受限孔径下输出应该有明显的艾里斑波动。



高斯光束，无调制



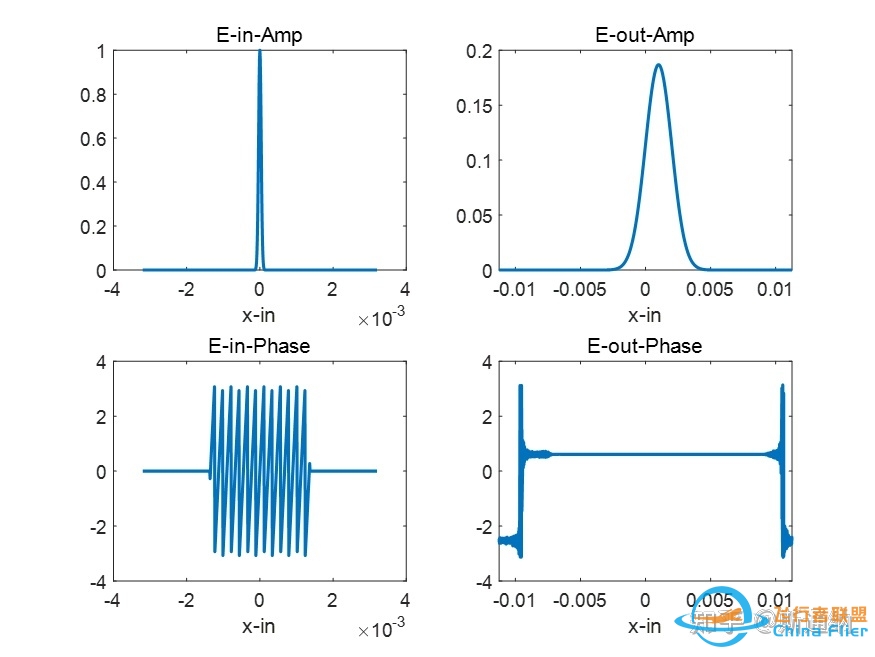
输入场经过闪耀光栅相位调制，输出光束中心偏移到+1衍射级位置



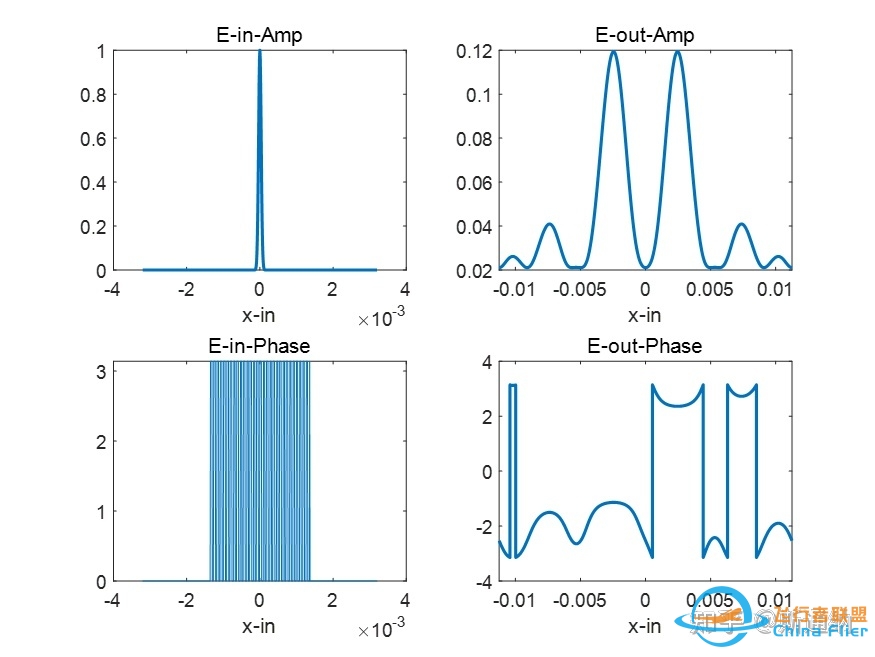
输入场经过二元光栅相位调制，输出场出现+1, -1级衍射



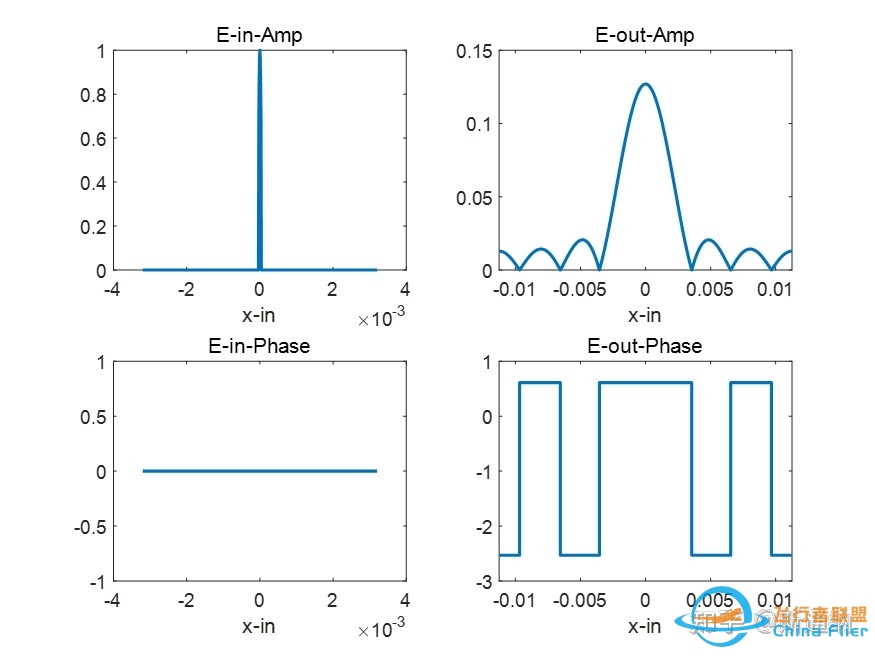
输入场加过矩形窗调制，输出场出现艾里斑

3、能量守恒

输入输出场的能量值要守恒，验证代码如下：
%% 能量守恒验证
I_in=E_in*E_in'*dxin
I_out=E_out*E_out'*dxout
I_res=I_out-I_in有两个点需要强调，
a、能量 I=\sum E\cdot E^{*}\cdot Δ
由于计算出的光场是功率密度函数，即每个值代表该点处的功率密度，为了求整个光场的能量，不能对计算出的光场直接求和，还需要乘上采样间隔Δ，使得能量守恒。
采样点越多，采样间隔越小，采样间隔与采样点数的乘积值应该为谱宽范围。
b、matlab特殊计算符号中，使用“ ' ”对复数向量或矩阵转置，维度发生转置时，其值也自动求共轭。
6、参考

[1] RayTransferMatrixDefinitions - Ray transfer matrix analysis - Wikipedia
[2] Picart P, Li J. Digital holography[M]. John Wiley & Sons, 2013.
[3] J. W. Goodman, Introduction to Fourier Optics 4th edition, 2017.
[4] 管致中, 夏恭恪, 孟桥. 信号与线性系统.第6版[M]. 高等教育出版社, 2015.